WZX's Blog

深层神经网络中的正则化

2018/12/20 MachineLearning 共 1127 字，约 4 分钟

随着神经网络的深度化，容易出现训练集的精度高，测试集的精度相对不高，这可能是出现了过拟合的情况。这时可以通过增加训练集来解决。如果增加训练集的代价太高，正则化是一个很好的选择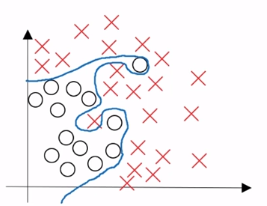

L1、L2正则化

数学符号

  • L1范数
\[||W||_{1}= \sum_{i}\sum_{j}|w_{ij}|\]
  • L2范数
\[||W||_{2}=\sqrt{\sum_{i}\sum_{j}w_{ij}^2} \\||W||_{2}^2=\sum_{i}\sum_{j}w_{ij}^2\]
  • \(\lambda\) ： 控制正则化程度的参数

原理

成本函数增添 L2正则项

\[J_{L2} = J(w,b) +\frac{1}{m}\frac{\lambda}{2}\sum_{l}|| W ||_{2}^2\]

这样一来，模型越复杂，正则项值就越大，成本函数就越大。用梯度下降算法更新时，参数的值便会减小，从而减弱神经网络对输出值的影响，最终减少过拟合的情况

例如更新参数 \(w_{ij}^{[l]}\) 时

\[\begin{equation} \begin{aligned} w_{ij}^{[l]}:&=w_{ij}^{[l]}-\alpha\frac{\partial{J_{L2}}}{\partial{w_{ij}^{[l]}}} \\&=w_{ij}^{[l]}-\alpha\frac{\partial{J}}{\partial{w_{ij}^{[l]}}}-\alpha\frac{\partial{(\frac{1}{m}\frac{\lambda}{2}\sum_{l} || W ||_{2}^2})}{\partial{w_{ij}^{[l]}}} \\&=w_{ij}^{[l]}-\alpha\frac{\partial{J}}{\partial{w_{ij}^{[l]}}}-\alpha\frac{\lambda}{m}w_{ij}^{[l]} \end{aligned} \end{equation}\]

这里是把 L2范数的平方 替换为 L1范数，就是 L1正则化的公式

Dropout

原理

在每次迭代中，随机的使一些节点失活，从而减弱神经网络对输出值的影响，最终减少过拟合的情况。听起来很像佛系正则化，但经过实践证明，这个方法确实有效果

如何实现

这个比较简单，引入一个参数 keep_knob，1−keep_knob 表示失活率

  • 正向传播时，除输入层与输出层外，按失活率使节点失活，并记录下这些节点的位置
  • 反向传播时，将正向传播记录的位置的节点的梯度值，置为0
  • 将每层的输出值除以 keep_knob，确保最终成本函数的结果仍然具有正则化前的预期值

demo

Deep Neural Network Demo

文档信息

Search

    Table of Contents