Dynamic Time Warping(DTW) 是一种衡量两个时间序列之间的相似度的方法。主要用来解决两个时间序列不“同步”的问题。DTW 使序列在时间维度上非线性地“扭曲”以确定他们的相似度,并且独立于非线性的时间维度变化。
原理
在时间序列中,需要比较相似性的两段时间序列的长度可能并不相等,在语音识别领域表现为不同人的语速不同。因为语音信号具有相当大的随机性,即使同一个人在不同时刻发同一个音,也不可能具有完全的时间长度。而且同一个单词内的不同音素的发音速度也不同,比如有的人会把“A”这个音拖得很长,或者把“i”发的很短。
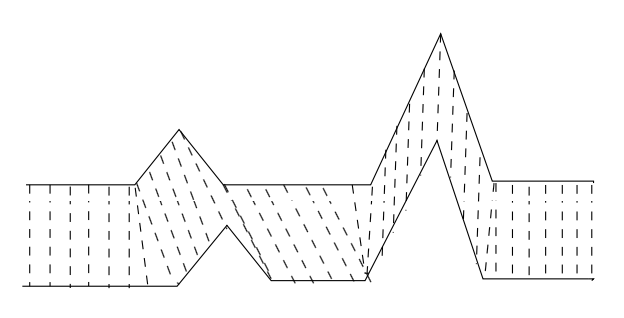
DTW 通过扭曲时间序列,使时间序列沿时间轴延伸和缩短,然后再比较相似性。
约束
总的来说,DTW 是一个计算两个时间序列的最优匹配的方法,但要满足以下约束:
第一个序列的每个索引必须要匹配另一个序列的一个或多个索引,反之亦然
第一个序列的第一个索引必须匹配另一个序列的第一个索引(但是这不是它的唯一匹配)
第一个序列的最后一个索引必须匹配另一个序列的最后一个索引(但是这不是它的唯一匹配)
第一个序列与另一个序列的索引映射必须单调增加,反之亦然。比如说,如果 $j>i$ 是第一个的序列里的两个索引,那么在另一个序列中将不会存在两个序列 $l>k$ ,索引 $i$ 匹配索引 $l$,并且索引 $j$ 匹配索引 $k$。反之亦然
记 cost 为每个匹配的索引对的距离的总和。最优匹配 即是满足约束的,且 cost 为最小的匹配。
实现
构造距离矩阵
假设我们有两个序列
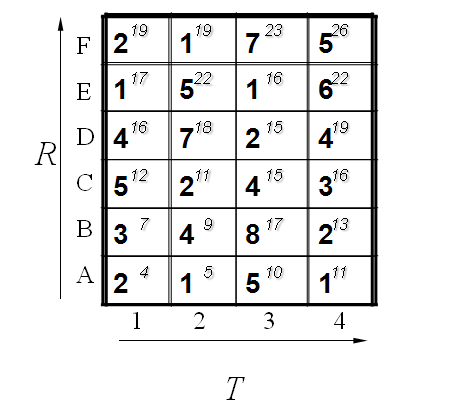
\[Q = \left\{ \begin{matrix} q_{1} \\ \vdots \\ q_{n} \\ \end{matrix} \right\} \qquad P = \left\{ \begin{matrix} p_{1} \\ \vdots \\ p_{n} \\ \end{matrix} \right\}\]为了对齐这两个序列,我们需要构造一个 $n \times m$ 的矩阵网格,矩阵元素 $(i, j)$ 表示 $q_i$ 和 $p_j$ 两个点的距离 $d(q_i, p_j)$。下面我们只要寻找一条通过此网格中若干格点的路径,路径通过的格点即为两个序列进行计算的对齐的点。
特别地,如果这两个序列并不是一维的序列,我们只需分别构造各维度间的距离矩阵,并求和。使用Numpy库可以很好地实现这一过程
# 欧氏距离
np.sum((x[:, None, :] - y[None, :, :]) ** 2, axis=2)
计算损失矩阵
由于对最优匹配的约束,每一个格点至下一个各点的路径只有三个方向了。例如如果路径已经通过了格点 $(i, j)$,那么下一个通过的格点只可能是下列三种情况之一:$(i+1, j)$,$(i, j+1)$ 或者 $(i+1, j+1)$。我们就可以由此计算出损失矩阵(Cost Matrix)
对于损失矩阵 $M_c$ ,我们对距离矩阵 $M$ 按顺序依次遍历,逐步计算出每个 $M_c(i,j)$ 的值。遵循以下公式:
\[M_c(i,j)=M(i,j)+min(M_c(i-1,j−1),M_c(i−1,j),M_c(i,j−1))\]在编程实现时,我们可以对距离矩阵扩充以便于运算
\[\left\{ \begin{matrix} 0 & \infty & \cdots & \infty \\ \infty & m_{11} & \cdots & m_{1n} \\ \vdots & m_{21} & \cdots & m_{2n} \\ \infty & m_{m1} & \cdots & m_{mn} \\ \end{matrix} \right\}\]搜索路径
在上一步时,就已经完成了路径的搜索,我们只需反向推导,即可求出距离
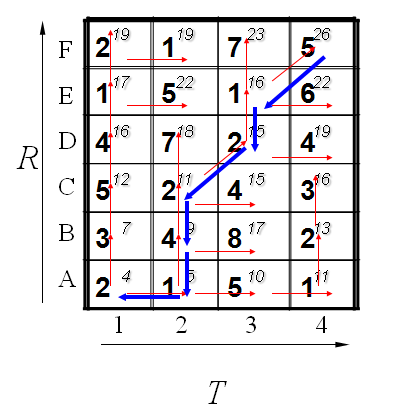
代码实现
Reference
[1] Dynamic time warping. Wikipedia, 2019.
[2] MILLER A. A python/numpy/cython implementation of dynamic time warping (DTW) for aligning time series. Github. 2017.
[3] 算法笔记-DTW动态时间规整 - Raymond Kwan - CSDN博客[EB/OL]. 2015.
文档信息
- 本文作者:wzx
- 本文链接:https://masterwangzx.com/2019/02/06/dtw/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)