刚开始接触数据结构,之前只对顺序表,链表,栈和队列有些接触,对二叉树这个概念还是很陌生,所以总结一下
定义
树
树是 $n$ 个结点的有限集。$n=0$ 时称为空树
元素
- 结点
- 根结点
- 父结点
- 子结点
- 最左子结点
- 兄弟结点
- 左兄弟结点
- 右兄弟结点
- 分支结点:非终端结点
- 叶结点:终端结点
- 祖先
- 后代
- 边:两个父子结点的有序对
- 路径:多条相邻边的集合
- 子树:当 $n>1$ 时,其余结点可分为 $m$ 个互不相交的有限集
属性
- 层数:根结点为第0层
- 深度:层数最大的叶结点的层数
- 高度:深度+1
- 结点度:结点拥有的子树数
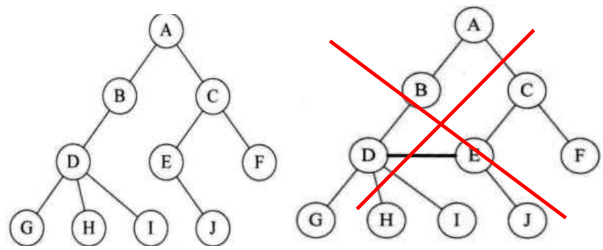
二叉树
Binary Tree
二叉树是 $n(n>=0)$ 个结点的有限集合,由一个根节点和两棵互不相交的,称为左子树和右子树的二叉树组成
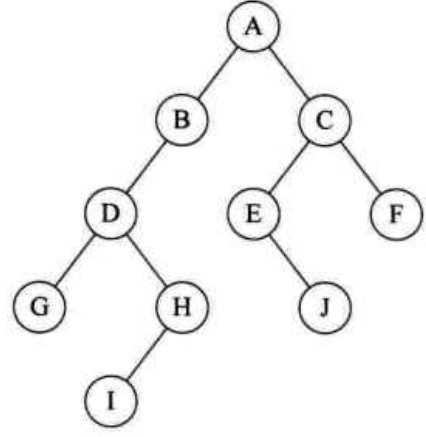
满二叉树
Full Binary Tree
所有的分支结点都存在左子树和右子树,并且所有叶子都在同一层上
二叉搜索树
Binary Search Tree(BST)
- 节点的左子树只包含小于当前节点的数。
- 节点的右子树只包含大于当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
完全二叉树
Complete Binary Tree
对一棵具有 $n$ 个结点的二叉树按层序编号,编号为i的结点与同样深度的满二叉树中编号为 $i$ 的结点在二叉树中位置完全相同
- 最多只有最下面的两层结点度数可以小于2
- 最下一层的结点都集中最左边
不太好理解完全二叉树的概念。通俗一点说,即除了最后一层外,每一层上的节点数均达到最大值;在最后一层上只缺少右边的若干结点。所以,满二叉树一定是完全二叉树但完全二叉树不一定是满的
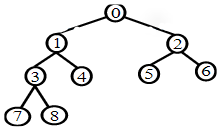
如下图所示,一个完全二叉树,但如果少了10这个结点,就不是完全二叉树了 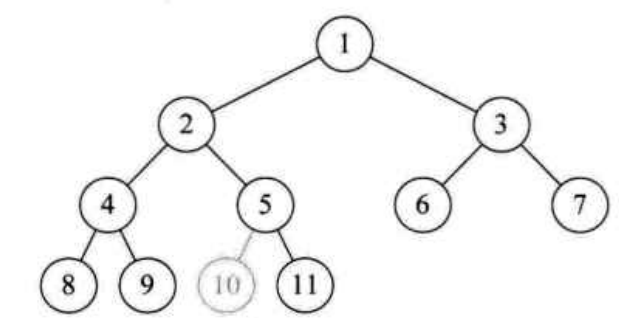
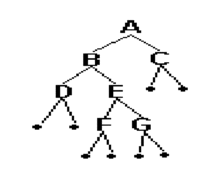
扩充二叉树
二叉树中出现空子树的位置增加空树叶,所形成的二叉树
从扩充的二叉树的根到每个外部结点的路径长度之和称为外部路径长度(E),扩充的二叉树里从根到每个内部结点的路径长度之和称为内部路径长度(I),它们之间的关系满足 $E=I+2N$(N为内部结点数)
性质
在二叉树中,第 $i$ 层上最多有 $2^i$ 个结点( $i\ge 0$ )
深度为 $k$ 的二叉树至多有 $2^{k+1}-1$ 个结点( $k\ge0$ )
一棵二叉树,若其叶结点数为 $n_0$,结点度数为2的结点数为 $n_2$,则 $n_0=n_2+1$
满二叉树定理:非空满二叉树的叶结点数等于其分支结点数加1
有 $n$ 个结点的完全二叉树的叶结点个数为 $\lfloor \frac{n+1}{2} \rfloor$
有 $n$ 个结点的完全二叉树的高度为 $\lfloor log_2n \rfloor+1$
有 $n$ 个结点的完全二叉树的节点按层序编号(起始索引为0),对于任意结点 $i$ :
- 当 $0<i<n$,则其父结点为 $\lfloor \frac{i-1}{2} \rfloor$,故其左子结点为 $2i+1$,右子结点为$2i+2$
- 当 $i$ 为偶数且 $0<i<n$,为右结 点,则左兄弟结点为 $i-1$,否则没有左兄弟
- 当 $i$ 为奇数且 $i+1<n$,为左结点,则右兄弟结点为 $i+1$,否则没有右兄弟
对于第7条性质,可以作以下推导,设当前结点在第 $k$ 层的第 $j$ 个
- 当前结点的索引为 $2^k-2+j$
- 左子结点索引:$2^{k+1}-2+2(j-1)+1=2^{k+1}+2j-3$
- 右子结点索引:$2^{k+1}-2+2(j-1)+2=2^{k+1}+2j-2$
所以,$\lfloor \frac{2^{k+1}+2j-3-1}{2} \rfloor=\lfloor \frac{2^{k+1}+2j-2-1}{2} \rfloor=2^k-2+j$
遍历
二叉树的遍历就是二叉树结点的线性化
表达式的二叉树的前序遍历和后序遍历的结果就是前缀和后缀表达式
前序遍历
当到达某个结点时,先输出该结点,再访问左子结点,最后访问右子结点
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> res = new LinkedList<>();
recursion(root, res);
return res;
}
private void recursion(TreeNode root, List<Integer> res) {
if (root == null) return;
res.add(root.val);
recursion(root.left, res);
recursion(root.right, res);
}
非递归实现
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> res = new LinkedList<>();
if (root == null) return res;
Deque<TreeNode> stack = new LinkedList<>();
stack.addFirst(root);
while (!stack.isEmpty()) {
TreeNode node = stack.pollFirst();
// 先访问根结点
res.add(node.val);
// 注意左右子结点的入栈顺序
if (node.right != null) stack.addFirst(node.right);
if (node.left != null) stack.addFirst(node.left);
}
return res;
}
中序遍历
当到达某个结点时,先访问左子结点,再输出该结点,最后访问右子结点
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new LinkedList<>();
recursion(root, res);
return res;
}
private void recursion(TreeNode root, List<Integer> res) {
if (root == null) return;
recursion(root.left, res);
res.add(root.val);
recursion(root.right, res);
}
非递归实现
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new LinkedList<>();
// (结点,该节点是否访问过左子树)
Deque<Map.Entry<TreeNode, Boolean>> stack = new LinkedList<>();
if (root != null) stack.addFirst(new AbstractMap.SimpleEntry<>(root, false));
while (!stack.isEmpty()) {
Map.Entry<TreeNode, Boolean> entry = stack.peekFirst();
boolean left = entry.getValue();
TreeNode node = entry.getKey();
if (!left) {
// 没有访问过左子树,先访问左子树再访问当前结点
entry.setValue(true);
if (node.left != null) stack.addFirst(new AbstractMap.SimpleEntry<>(node.left, false));
} else {
// 访问过左子树,先访问当前结点再访问右子树
res.add(node.val);
stack.removeFirst();
if (node.right != null) stack.addFirst(new AbstractMap.SimpleEntry<>(node.right, false));
}
}
return res;
}
后序遍历
当到达某个结点时,先访问左子结点,再访问右子结点,最后输出该结点
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new LinkedList<>();
recursion(root, res);
return res;
}
private void recursion(TreeNode root, List<Integer> res) {
if (root == null) return;
recursion(root.left, res);
recursion(root.right, res);
res.add(root.val);
}
非递归实现
private enum State{
// 左子结点没有访问
LEFT,
// 右子结点没有访问
RIGHT,
// 结点没有访问
CUR
}
public List<Integer> postorderTraversal2(TreeNode root) {
List<Integer> res = new LinkedList<>();
// (结点, 该节点的访问状态)
Deque<Map.Entry<TreeNode, State>> stack = new LinkedList<>();
if (root != null) stack.addFirst(new AbstractMap.SimpleEntry<>(root, State.LEFT));
while (!stack.isEmpty()) {
Map.Entry<TreeNode, State> entry = stack.peekFirst();
TreeNode node = entry.getKey();
State state = entry.getValue();
if (state == State.LEFT) {
// 先访问左子树
entry.setValue(State.RIGHT);
if (node.left != null) stack.addFirst(new AbstractMap.SimpleEntry<>(node.left, State.LEFT));
} else if (state == State.RIGHT) {
// 再访问右子树
entry.setValue(State.CUR);
if (node.right != null) stack.addFirst(new AbstractMap.SimpleEntry<>(node.right, State.LEFT));
} else {
// 最后访问当前结点
res.add(node.val);
stack.removeFirst();
}
}
return res;
}
层序遍历
广度优先的算法,所以使用队列实现
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> res = new LinkedList<>();
Deque<TreeNode> queue = new LinkedList<>();
if (root != null) queue.addFirst(root);
while (!queue.isEmpty()) {
int size = queue.size();
List<Integer> layer = new LinkedList<>();
for (int i = 0; i < size; i++) {
TreeNode node = queue.pollLast();
layer.add(node.val);
if (node.left != null) queue.addFirst(node.left);
if (node.right != null) queue.addFirst(node.right);
}
res.add(layer);
}
return res;
}
重建
二叉树的先跟、中根和后根序列中的任何一个都不能唯一确定一棵二叉树,必须要组合使用
先跟+中根
- 先跟序列的第一个元素为根结点
- 中根序列={左子树的中根序列+根结点+右子树的中根序列}
- 先跟序列={根结点+左子树的先跟序列+右子树的先跟序列}
public TreeNode buildTree(int[] preorder, int[] inorder) {
// 中根序列的倒排索引,加速查找
Map<Integer, Integer> InvertedIndex = new HashMap<>(inorder.length);
for (int i = 0; i < inorder.length; i++) {
InvertedIndex.put(inorder[i], i);
}
return recursion(preorder, 0, preorder.length - 1, 0, inorder.length - 1, InvertedIndex);
}
private TreeNode recursion(int[] preorder, int preBegin, int preEnd, int InBegin, int InEnd, Map<Integer, Integer> InvertedIndex) {
if (preBegin > preEnd) return null;
// 由先跟序列得到root
int rootVal = preorder[preBegin];
TreeNode root = new TreeNode(rootVal);
// 在中根序列中找到root
int inRootIndex = InvertedIndex.get(rootVal);
// 左右子树长度
int leftNum = inRootIndex - InBegin;
int rightNum = InEnd - inRootIndex;
root.left = recursion(preorder, preBegin + 1, preBegin + leftNum, InBegin, inRootIndex - 1, InvertedIndex);
root.right = recursion(preorder, preEnd - rightNum + 1, preEnd, inRootIndex + 1, InEnd, InvertedIndex);
return root;
}
中根+后根
- 后根序列的最后一个元素是根结点
- 中根序列={左子树的中根序列+根结点+右子树的中根序列}
- 后跟序列={左子树的后根序列+右子树的后根序列+根结点}
public TreeNode buildTree(int[] inorder, int[] postorder) {
// 中根序列的倒排索引,加速查找
Map<Integer, Integer> invertedIndex = new HashMap<>(inorder.length);
for (int i = 0; i < inorder.length; i++) {
invertedIndex.put(inorder[i], i);
}
return recursion(0, inorder.length - 1, postorder, 0, postorder.length - 1, invertedIndex);
}
public TreeNode recursion(int inBegin, int inEnd, int[] postorder, int postBegin, int postEnd, Map<Integer, Integer> invertedIndex) {
if (inBegin > inEnd) return null;
// 由后根序列得到root
int rootVal = postorder[postEnd];
TreeNode root = new TreeNode(rootVal);
// 中根序列中找到root
int inRootIndex = invertedIndex.get(rootVal);
// 左右子树长度
int leftNum = inRootIndex - inBegin;
int rightNum = inEnd - inRootIndex;
root.left = recursion(inBegin, inRootIndex - 1, postorder, postBegin, postBegin + leftNum - 1, invertedIndex);
root.right = recursion(inRootIndex + 1, inEnd, postorder, postEnd - 1 - rightNum + 1, postEnd - 1, invertedIndex);
return root;
}
先根+后根
- 先跟序列={根结点+左子树的先跟序列+右子树的先跟序列}
- 后跟序列={左子树的后根序列+右子树的后根序列+根结点}
- 先跟序列中,左子树先根序列的首个元素为根结点的左子结点,右子树先跟序列的首个元素为根结点的右子结点
- 后根序列中,左子树后根序列的末尾元素为根结点的左子结点,右子树后根序列中的末尾元素为根结点的右子结点
public TreeNode constructFromPrePost(int[] pre, int[] post) {
// 后跟序列的倒排索引,加速查找
Map<Integer, Integer> invertedIndex = new HashMap<>(pre.length);
for (int i = 0; i < post.length; i++) {
invertedIndex.put(post[i], i);
}
return recursion(pre, 0, pre.length - 1, 0, pre.length - 1, invertedIndex);
}
private TreeNode recursion(int[] pre, int preBegin, int preEnd, int postBegin, int postEnd, Map<Integer, Integer> invertedIndex) {
if (preBegin > preEnd) return null;
if (preBegin == preEnd) return new TreeNode(pre[preBegin]);
// 在先根序列中找到root和其左子结点,默认左子树优先存在
int rootVal = pre[preBegin];
TreeNode root = new TreeNode(rootVal);
int leftVal = pre[preBegin + 1];
// 在后根序列中找到root左子结点
int postLeftIndex = invertedIndex.get(leftVal);
// 左右子树长度
int leftNum = postLeftIndex - postBegin + 1;
int rightNum = postEnd - 1 - postBegin + 1 - leftNum;
root.left = recursion(pre, preBegin + 1, preBegin + leftNum, postBegin, postBegin + leftNum - 1, invertedIndex);
root.right = recursion(pre, preEnd - rightNum + 1, preEnd, postEnd - rightNum, postEnd - 1, invertedIndex);
return root;
}
Reference
[1]程杰. 大话数据结构[M]. 清华大学出版社, 2011.
[2]二叉树基础 - 北京大学[EB/OL]. Coursera.
[3]二叉树构建,先序,中序,后序遍历(以及非递归实现),广度优先遍历 - 腾讯云+社区[EB/OL].
文档信息
- 本文作者:wzx
- 本文链接:https://masterwangzx.com/2019/03/16/binary-tree/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)