从 最小化误差平方和 和 方程组的最小二乘解 两个角度理解最小二乘问题
最小化误差平方和
直线模型
我们要构造一条直线 $y=mx+b$ 来拟合 实验中产生的点 $(x_i,y_i)$。这样的话,对于每个数据点都会产生一个误差 $r_i=y_i-mx_i-b$。因为误差服从高斯分布,所以 $\chi^2 = \sum{r_i^2}$ 。我们要做的就是最小化这些误差
\[\nabla \chi^2 = \left[\begin{array}{c} \frac{\partial{\chi^2}}{\partial{m}} \\ \frac{\partial{\chi^2}}{\partial{b}} \end{array}\right] = \left[\begin{array}{c} 0 \\ 0 \end{array}\right] \\ \left[\begin{array}{c} m \\ b \end{array}\right]=\left[\begin{array}{c} \frac{\sum{(x-\overline{x})(y-\overline{y})}}{\sum{(x-\overline{x})^2}}\\ \overline{y}-m\overline{x} \end{array}\right]\]这样我们便得到了拟合的直线。
一般模型
我们构造这样一条曲线 $y=f(x;a_k;\sigma_i)$ 。其中 $w_i$ 是每个数据点的观测值(y)的可信度,$a_k$ 是曲线的若干参数。定义误差平方和为
\[\chi^2 = \sum{w_i(y_i-f(x;a_k;\sigma_i))^2}\]现在我们只要找到 $a_k$ 使得 $\chi^2$ 最小即可。可以使用梯度下降法求得 $a_k$ 的值
假设误差是独立的随机变量,均值为零,则一般取 $w_i=\frac{1}{\sigma_i^2}$ ,方差越大,可信度越小
方程组的解
最小二乘解
对于一个线性方程组 $A\boldsymbol{x}=\boldsymbol{b}$,在实际应用中,常出现不相容的系统。当系统要求一个解但却无解时,最好的办法是求 $\boldsymbol{x}$ 使 $A\boldsymbol{x}$ 尽可能的接近 $\boldsymbol{b}$
考虑 $A\boldsymbol{x}$ 作为 $\boldsymbol{b}$ 的逼近,所以 $| \boldsymbol{b}-A\boldsymbol{x} |$ 应该尽可能的小,这样我们便得出了最小二乘解 $\hat{\boldsymbol{x}}$ 的定义,对于 $A_{m\times n},\boldsymbol{b}\in R^n$
\[\| \boldsymbol{b}-A\hat{\boldsymbol{x}}\| \le \| \boldsymbol{b}-A\boldsymbol{x} \| ,\qquad \forall x\in R^n\]经过观察得出,向量 $A\boldsymbol{x}$ 必然在 $A$ 的列向量空间中,我们就是要找到 $\hat{\boldsymbol{x}}$ ,使得在 $Col\ A$ 中与 $\boldsymbol{b}$ 的距离最小的向量为 $A\hat{\boldsymbol{x}}$ 。
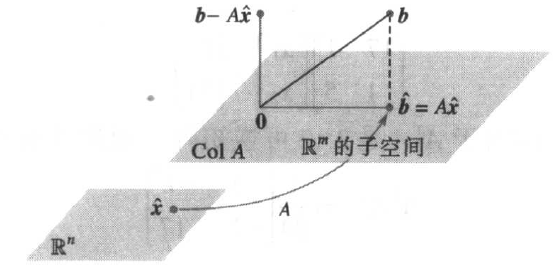
分析一下便知,若 $\hat{\boldsymbol{b}}=proj_{Col\ A}\boldsymbol{b}$ ,即 $\boldsymbol{b}$ 在 $Col\ A$ 上的正交投影,$\hat{\boldsymbol{b}}$ 便是我们要找的 $A\hat{\boldsymbol{x}}$。现在只需求解方程组 $A \hat{\boldsymbol{x}}=\hat{\boldsymbol{b}}$ ,就求得了最小二乘解。由于 $\hat{\boldsymbol{b}}$ 在 $Col\ A$ 上,所以该方程一定是相容的
在图上可以看出, $\boldsymbol{b}-\hat{\boldsymbol{b}}$ 正交于 $Col\ A$,于是 $\boldsymbol{b}-\hat{\boldsymbol{b}}$ 与 $A$ 的每一列都正交,可得
\[A^T(\boldsymbol{b}-A\hat{\boldsymbol{x}})=\boldsymbol{0} \\ A^TA\boldsymbol{x}=A^T\boldsymbol{b}\]这个方程称为 $A\boldsymbol{x}=\boldsymbol{b}$ 的 正规方程,且一定是相容的
当且仅当 $A$ 的各列线性无关时,$AA^T$可逆,正规方程有唯一的最小二乘解 $\hat{\boldsymbol{x}}$
\[\hat{\boldsymbol{x}} = (AA^T)^{-1}A^T\boldsymbol{b}\]直线模型
我们要构造一条直线 $y=\beta_0 +\beta_1x$ 来拟合 实验中产生的点 $(x_i,y_i)$。这条直线称为 $y$ 在 $x$ 上的回归直线, $\beta_0, \beta_1$ 称为回归系数。
构造方程组 $X\boldsymbol{\beta}=\boldsymbol{y}$ ,其中
\[X=\left[\begin{array}{cc} 1 & x_1 \\ 1 & x_2 \\ \vdots & \vdots \\ 1 & x_n \end{array}\right],\boldsymbol{\beta}=\left[\begin{array}{c} \beta_1 \\ \beta_2 \end{array}\right],\boldsymbol{y}=\left[\begin{array}{c} y_1 \\ y_2 \\ \vdots \\ y_n \end{array}\right]\]因为实际上这些试验点大部分都不落在直线上,所以这个方程组肯定无解,这时候我们就可以求这个方程组的最小二乘解,求得参数 $\boldsymbol{\beta}$ 构成的直线就是最小二乘直线
一般模型
记模型的参数为 $\boldsymbol{\beta}$ ,建立类似的方程组, $\boldsymbol{y}=X\boldsymbol{\beta}+\boldsymbol{\epsilon}$ ,其中 $\boldsymbol{\epsilon} = \boldsymbol{y}-X\boldsymbol{\beta}$ ,为剩余向量。对于这个模型,我们需要最小化剩余向量的长度,根据最小二乘解的定义,相当于求 $X\boldsymbol{\beta}=\boldsymbol{y}$ 的最小二乘解
设使用模型 $y=\beta_0f_0(x)+\beta_1f_1(x)+\cdots+\beta_kf_k(x)$ 来拟合数据,则我们需要求解方程 $X\boldsymbol{\beta}=\boldsymbol{y}$ 的最小二乘解,其中
\[X=\left[\begin{array}{cc} f_0(x_1) & f_1(x_1) & \cdots & f_k(x_1) \\ f_0(x_2) & f_1(x_2) & \cdots & f_k(x_2) \\ \vdots & \vdots & \ddots & \vdots \\ f_0(x_n) & f_1(x_n) & \cdots & f_k(x_n) \end{array}\right],\boldsymbol{\beta}=\left[\begin{array}{c} \beta_1 \\ \beta_2 \\ \vdots \\ \beta_n \end{array}\right],\boldsymbol{y}=\left[\begin{array}{c} y_1 \\ y_2 \\ \vdots \\ y_n \end{array}\right]\]加权模型
若每个观测值(y)存在可信度 $w_i$,根据上述的一般模型,目标是使 $\sum w_i^2(y_i-\hat{y_i})^2$ 最小,将加权最小二乘可以转化为普通最小二乘模型
\[W=\left[\begin{array}{cc} w_1 & 0 & \cdots & 0 \\ 0 & w_2 & & 0 \\ \vdots & & \ddots & \\ 0 & 0 & \cdots & w_n \end{array}\right] \\ WA\boldsymbol{x}=W\boldsymbol{y}\]则正规方程为
\[(WA)^TWA\boldsymbol{x}=(WA)^TW\boldsymbol{y}\]REFERENCE
[1]莱. 线性代数及其应用[M]. 刘深泉 等, 译. 机械工业出版社, 2005.
文档信息
- 本文作者:wzx
- 本文链接:https://masterwangzx.com/2019/04/17/least-square/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)