WZX's Blog

直方图均衡化

2019/07/10 Others 共 2364 字，约 7 分钟

直方图是多种空间域处理技术的基础。直方图均衡化是将一幅图像的像素倾向于占据整个可能的灰度级并且分布均匀，这样处理过后的图像具有高对比度并且较高的还原了灰度细节

符号定义

  • $r$ ：原图像中某个像素点的灰度值， $0\le r \le L-1$
  • $s$ ：与r对应的输出灰度值， $0\le r \le L-1$
  • $T(r)$ ：变换 $T(r) = s$
  • $h(s)$ ：$T(r)$ 的反函数

设 $M,N$ 为图像的行和列的维数，$n$ 为像素点为某个灰度值的个数，则定义概率 $p(n) = \frac{n}{MN}$

  • $p_s(s)$ ：随机变量 $s$ 的概率密度函数
  • $p_r(r)$ ：随机变量 $r$ 的概率密度函数

限制条件

  • $T(r)$ 在 $0\le r \le L-1$ 上严格单调递增，保证输出值不少于对应输入值，并且存在反函数
  • $0\le r \le L-1$ 时，$0\le T(r) \le L-1$

转化函数

由密度函数变换公式可知（不知道的可以翻翻概率论课本了），变换后的 $s$ 的概率密度函数

\[p_s(s)=p_r(h(s))|h'(s)|\]

转化函数就是

\[s=T(r)=(L-1)\int_0^rp_r(w)dw\]

公式后半部分的积分就是r的概率分布函数。有定义可知，该转化函数满足限制条件，并且运用上面的公式推导变换后 $s$ 的概率密度函数

\[\begin{equation} \begin{aligned} p_s(s)&=p_r(h(s))|h'(s)| \\&=p_r(r)|\frac{1}{(L-1)p_r(r)}| \\&= \frac{1}{(L-1)},\qquad 0\le s \le L-1 \end{aligned} \end{equation}\]

可以看出，经过这个转化函数后，图像的像素服从均匀分布

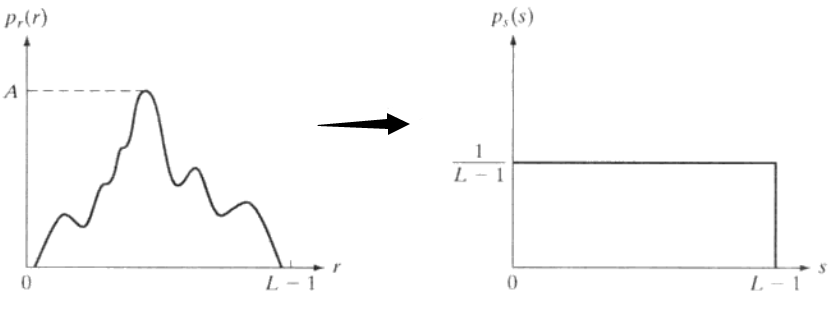
下面直接给出对于离散值的转化函数

\[\begin{equation} \begin{aligned} s_k=&T(r_k) \\&=(L-1)\sum_{j=0}^kp_r(r_j) \\&=\frac{L-1}{MN}\sum^k_{j=0}n_j,\qquad 0\le r \le L-1 \end{aligned} \end{equation}\]

代码实现

如此经典的算法，opencv肯定已经帮我们实现好了，代码很简单

import cv2
from matplotlib import pyplot as plt
import numpy as np

# 读取的文件是BGR三通道的黑白图
origin_three = cv2.imread('test.jpg', cv2.IMREAD_UNCHANGED)
# 转化成RGB
origin_three = origin_three[:, :, ::-1]
# 转化单通道
origin_one = origin_three[:, :, 0]

# 直方图均衡化
processed = cv2.equalizeHist(origin_one)

# 转化为三通道
processed = processed[:, :, np.newaxis]
processed = np.concatenate([processed, processed, processed], axis=2)

# 对比显示
plt.figure()
plt.subplots_adjust(wspace=0.32, hspace=0.4)

plt.subplot(221)
plt.axis('off')
plt.imshow(origin_three)

plt.subplot(222)
plt.hist(origin_one.reshape(-1), bins=256, range=[0, 256], density=True)
plt.xlim(0, 255)
plt.xlabel("$r$")
plt.ylabel("$p_r(r)$")

plt.subplot(223)
plt.axis('off')
plt.imshow(processed)

plt.subplot(224)
plt.hist(processed[:, :, 0].reshape(-1), bins=256, range=[0, 256], density=True)
plt.xlim(0, 255)
plt.xlabel("$r$")
plt.ylabel("$p_r(r)$")

plt.show()

其实自己用代码实现的话也很简单，因为数据离散的，应用离散的转化函数即可，下面用 numpy 实现的直方图均衡化

processed = np.zeros(origin_one.shape, dtype=np.int)
hist, bins = np.histogram(origin_one, bins=256, range=[0, 256])
for i in range(1, len(hist)):
    hist[i] += hist[i - 1]
bins = bins.astype(int)
hist = 255 / (origin_one.shape[0] * origin_one.shape[1]) * hist
hist = hist.astype(int)
func = dict(zip(bins[:-1], hist))
for i in range(origin_one.shape[0]):
    for j in range(origin_one.shape[1]):
        processed[i, j] = func[origin_one[i, j]]

源图像地址

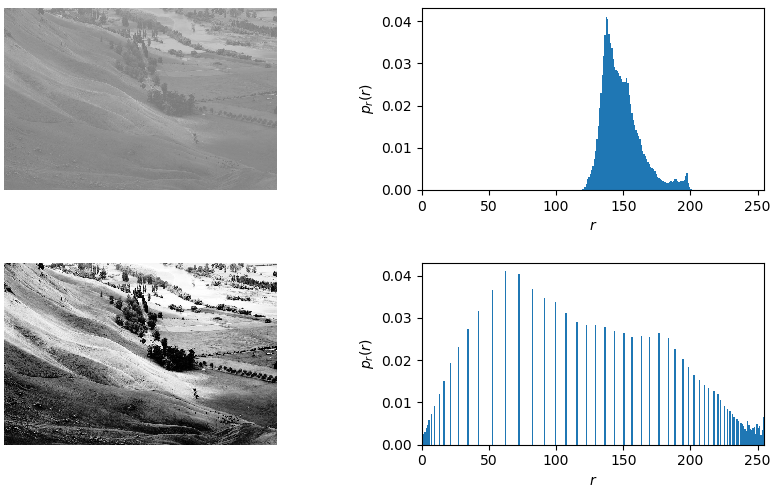
由图可以看出，直方图均衡导致的对比度增强可以补偿图像在视觉上难以区分灰度级的差别

这里有个小插曲，因为原图像是三通道的黑白图，而直方图均衡化只能处理单通道灰度图，所以之前要经过转化，并且三通道的黑白图和相同值的单通道灰度图显示效果是不一样的

REFERENCE

[1]冈萨雷斯. 数字图像处理[M]. 阮秋琦, 译. 电子工业出版社, 2011.

文档信息

Search

    Table of Contents