森林相比二叉树要更复杂，所以将森林与二叉树一起考虑将更好

定义

森林:零棵或多棵不相交的树的集合（通常是有序)

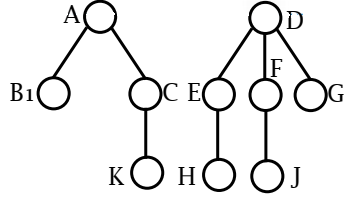
森林与二叉树的转化

二叉树为森林的 左子-右兄的二叉链表示法

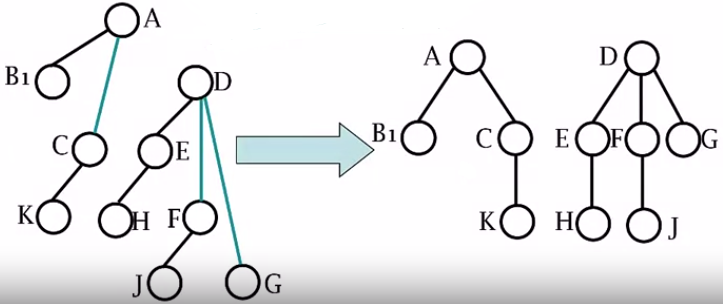
森林转二叉树

1. 树的所有兄弟结点连线（各个树的根结点当做兄弟结点处理）
2. 每个结点只保留之前 其第一个子结点的所有连线

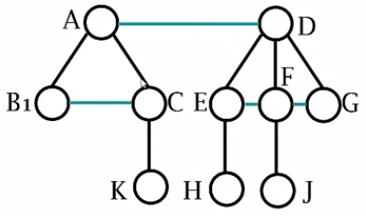
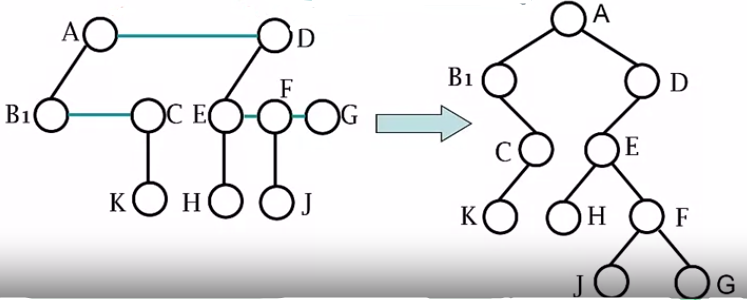
二叉树转森林

1. 若x结点是y结点的左子结点，则y与x的右子结点，x右子结点的右子结点…连线
2. 去掉之前与右子结点的连线

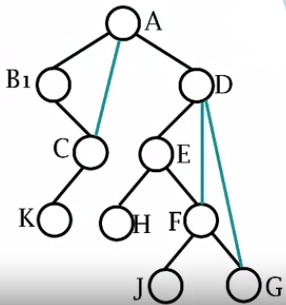
森林遍历

可以与之前所述的二叉树遍历对比

由于树存在多个子结点，无法明确规定根为哪两个子结点之间

前序遍历

与对应二叉链的前序遍历一致

void preOrderTraverse(TreeNode* T) {
	while (T != NULL) {
		std::cout << T->data;
		preOrderTraverse(T->leftMostChild);
		T = T->rightSibling;
	}
}

后序遍历

与对应二叉链的中序遍历一致

void postOrderTraverse(TreeNode* T) {
	while (T != NULL) {
		postOrderTraverse(T->leftMostChild);
		std::cout << T->data;
		T = T->rightSibling;
	}
}

层次遍历

深度优先算法，借助辅助队列实现

void SeqTraverse(TreeNode* T) {
	queue<TreeNode*> aQueue;
	TreeNode* pointer = T;

	while (pointer != NULL) {
		aQueue.push(pointer);
		pointer = pointer->rightSibling;
	}

	while (!aQueue.empty()) {
		pointer = aQueue.front();
		aQueue.pop();
		std::cout << pointer->data;

		pointer = pointer->leftMostChild;
		while (pointer != NULL) {
			aQueue.push(pointer);
			pointer = pointer->rightSibling;
		}
	}
}

森林的顺序存储

当需要将森林存储到外存之中时，我们需要将森林序列化，以顺序表的形式存储，这就要求我们能够将森林还原

我们通常将森林以二叉链的形式保存，二叉树的左子结点为原最左子结点，右子结点为原右兄弟节点，所以一般有下几种表示方法

• 带右链的先根次序表示
  • 森林的先根序列(二叉树的先根序列)
  • 每个顺序表位置的属性
    • info(结点值)
    • rlink(右兄弟指针)
    • ltag(是否有最左子结点)
• 带双标记的先根次序表示
  • 森林的先根序列(二叉树的先根序列)
  • 每个顺序表位置的属性
    • info(结点值)
    • rtag(是否有兄弟指针)
    • ltag(是否有最左子结点)
  • 恢复规则：假设AB两个连续结点
    • 若A的ltag为真，B就为A的左子结点
    • 若A的rtag为真，A压栈
    • 若A的ltag为假，弹栈，B为距离最近的有右结点的元素的右结点
• 带双标记的层次次序表示
  • 森林的层次序列
  • 每个顺序表位置的属性
    • info(结点值)
    • rtag(是否有兄弟指针)
    • ltag(是否有最左子结点)
  • 恢复规则：假设AB两个连续结点
    • 若A的rtag为真，B就为A的右结点
    • 若A的ltag为真，A入队
    • 若A的rtag为假，出队，B为距离最远的有左结点的元素的左结点
• 带度数的后根次序表示
  • 森林的后跟序列(二叉树的中根序列)
  • 每个顺序表位置的属性
    • info(结点值)
    • degree(度数)
  • 恢复规则：
    • 持续压栈，直到遇到度数不为0的结点，弹出其度数个数的结点，作为其子结点

并查集(Union-Find)

在对多个等价关系进行处理时，我们可以利用森林来实现归并和查找，每棵树代表一个等价类。由于主要关注树的根结点，所以应该至少有以下几个数据域

• 父指针数组int parents[]
• int count[]保存每个树的结点数
• num保存结点的个数

如果有需要还可以再开个数组保存结点的值

查找

给定一个结点，递归找到其所在子树的根结点

如果运用路径压缩，在查找后，将其作为根结点的子结点，目的是减少树的层数，从而减少寻找父结点的时间

int find(int x) {
	if (parents[x] == x) {
		return x;
	}
	// 路径压缩
	parents[x] = find(parents[x]);
	return parents[x];
}

归并

出现了一个新的等价关系，我们需要根据这个等价关系对森林做出调整

1. 递归的查找到两个结点所在子树的根结点
2. 若根结点不相同，则将数量较少的树的根结点作为另一个树的子结点

这是加权归并，目的是减少树的层数，从而减少寻找父结点的时间

void aUnion(int x, int y) {
	int root1 = find(x);
	int root2 = find(y);

	// 加权合并
	if (count[root1] < count[root2]) {
		int temp = root1;
		root1 = root2;
		root2 = temp;
	}
	parents[root2] = root1;
	count[root1] += count[root2];
}

REFERENCE

1. 树的定义、树与二叉树的等价转换
2. 树的顺序存储和K叉树