内排序算法的实现和比较
概念
- 排序对象
- 序列(sequence):线性表
- 记录(record):排序的基本单位,组成序列
- 关键码(key):唯一确定记录的一个或多个数据域
- 排序码(sort key):排序的依据的一个或多个数据域
- 排序方法
- 内排序:排序过程在内存中完成
- 外排序:
- 评价指标
- 稳定性:多个具有相同排序码的记录排序后相对位置是否不变
- 时间复杂度
- 空间复杂度
插入排序
直接插入排序
不断将一个记录插入到一个排序好的有序表中的合适位置
void sortArray(vector<int>& nums) {
int length = nums.size();
for (int i = 1; i < length; i++) {
int record = nums[i];
int j = i - 1;
// 空出插入record的位置
while (j >= 0 && nums[j] > record) {
nums[j + 1] = nums[j];
j--;
}
// 插入
nums[j + 1] = record;
}
}
shell排序
应用跳跃分割对序列进行分组,对小序列进行插入排序。逐渐减少跳跃的间距,直至对整体进行插入排序,如下所的增量序列
- Hibbard增量序列:${2^k-1,2^{k-1}-1,\cdots,7,3,1}$
- Shell(3):以3为间隔
最坏 $\Theta(n^{3 \backslash 2})$
void sortArray(vector<int>& nums) {
int length = nums.size();
for (int delta = length/2; delta > 0; delta /= 2) {
// 遍历每个相距为delta的序列
for (int start = 0; start < delta; start++) {
// 以相距为delta的序列应用插入排序
for (int i = delta + start; i < length; i += delta) {
int record = nums[i];
int j = i - delta;
// 空出插入record的位置
while (j >= 0 && nums[j] > record) {
nums[j + delta] = nums[j];
j -= delta;
}
// 插入
nums[j + delta] = record;
}
}
}
}
选择排序
直接选择排序
每次选择最小的记录放在当前位置
void sortArray(vector<int>& nums) {
int length = nums.size();
for (int i = 0; i < length ; i++){
// 找到i之后最小的值
int minIndex = i;
int minValue = nums[i];
for (int j = i; j < length ; j++){
if(minValue>nums[j]){
minIndex = j;
minValue = nums[j];
}
}
// 交换
swap(nums[i], nums[minIndex]);
}
}
堆排序
利用最小堆
void sortArray(vector<int>& nums) {
int length = nums.size();
priority_queue<int> max_heap;
// 建堆
for (int i = 0; i < length; i++) {
max_heap.push(nums[i]);
}
for (int i = length - 1; i >= 0; i--) {
nums[i] = max_heap.top();
max_heap.pop();
}
}
交换排序
冒泡排序
不停地比较相邻的记录,如果不满足排序要求,就交换相邻记录,直到所有的记录都已经排好序
void sortArray(vector<int>& nums) {
int length = nums.size();
for (int i = 0; i < length - 1; i++) {
bool isSwap = false;
// 冒泡
for (int j = length - 1; j > i; j--) {
if (nums[j] < nums[j - 1]) {
// 交换
swap(nums[j], nums[j - 1]);
isSwap = true;
}
}
// 未发生交换说明已经全部排序完成
if (!isSwap) {
return;
}
}
}
快速排序
利用了分治的思想
- 选择轴值(pivot)
- 将序列划分为两个子序列L和R,使得L 中所有记录都小于或等于轴值,R中记录都大于轴值
- 对子序列L和R递归调用快速排序
void QuickSort(vector<int>& nums, int left, int right) {
if (left >= right) {
return;
}
// 选择轴值
int pivot = (right - left) / 2 + left;
int record = nums[pivot];
// 每次从左边或右边拿出大于或小于pivot的值放到对面
// 交替执行
int l = left;
int r = right;
nums[pivot] = nums[right];
while (l < r) {
while (nums[l] <= record && l < r) {
l++;
}
if (l < r) {
nums[r--] = nums[l];
}
while (nums[r] > record && l < r) {
r--;
}
if (l < r) {
nums[l++] = nums[r];
}
}
nums[l] = record;
QuickSort(nums, left, l - 1);
QuickSort(nums, l + 1, right);
}
轴值如何选择很关键
分配排序
计数排序
- 事先知道序列中的记录都位于某个小区间段内
- 由最大最小元素构建辅助数组;统计数组中每个值元素出现的次数,存入辅助数组中对应位置;从前往后,对所有计数进行累加;从后往前,反向填充目标数组
例如,待排数组:7,3,8,9,6,1,8’,1’,2
排序码计数:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 2 | 1 | 1 | 0 | 0 | 1 | 1 | 2 | 1 |
累加计数:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 2 | 3 | 4 | 4 | 4 | 5 | 6 | 8 | 9 |
这样我们就知道记录在排序序列的位置了,遍历原数组,按照累计计数依次放入对应位置
void bucketSort(vector<int>& array, int min, int max) {
int n = array.size();
// 辅助数组长度
int m = max - min + 1;
vector<int> count(m, 0);
vector<int> temp(n, 0);
for (int i = 0; i < n; i++) {
temp[i] = array[i];
}
// 统计每个元素的个数
for (int i = 0; i < n; i++) {
count[array[i] - min]++;
}
// 统计小于等于i的元素个数
for (int i = 1; i < m; i++) {
count[i] += count[i - 1];
}
// 从后向前,保证稳定性
for (int i = n - 1; i >= 0; i--) {
array[--count[temp[i] - min]] = temp[i];
}
}
桶排序
将原数组分割为多个桶,桶为一个数据容器,存储一个区间内的数。对桶内的元素应用其他排序算法,再依次收集每个桶中的元素,顺序放置到输出序列中。
假设采用时间复杂度为 $O(nlogn)$ 的排序算法,当待排元素能平均地分配到每个桶中时,使用桶排序的平均时间复杂度为 $O(n+m\times \frac{n}{m}log \frac{n}{m})=O(nlog\frac{n}{m}+n)$ 。当取 $n=m$ ,可以取到最小时间复杂度 $O(n)$ ,但此时空间复杂度最高。
基数排序
高位指对记录大小影响较大,低位指对记录大小影响较小
若记录中含有多个排序码 $(k_{d-1},\cdots,k_1,k_0)$ ,就可以对每种排序码应用桶排序,就是基数排序,具体实现由高位优先法(MSD)和低位优先法(LSD)
由于次高位的排序会影响高位已经排好的大小关系,所以MSD使用递归分治的思想。由高至低递归分解至最小的桶,再将所有的桶连接起来
由于高位的排序不会影响次高位已经排好的大小关系,所以一般常用LSD。由低至高,依次对排序码应用计数排序。
// d:位数 radix:基数 minR:位最小值 maxR:位最大值
void RadixtSort(vector<int>& array, int d, int radix, int minR, int maxR) {
int n = array.size();
// 辅助数组长度
int r = maxR - minR + 1;
vector<int> count(r, 0);
vector<int> temp(n, 0);
// 对每一位应用计数排序
for (int i = 0; i <= d; i++) {
for (int j = 0; j < r; j++) {
count[j] = 0;
}
// 统计每个元素个数
for (int j = 0; j < n; j++) {
int k = array[j] / (int)pow(radix, i) % radix;
count[k - minR]++;
}
// 统计小于等于i的元素个数
for (int j = 1; j < r; j++) {
count[j] += count[j - 1];
}
for (int j = 0; j < n; j++) {
temp[j] = array[j];
}
// 从后向前,保证稳定性
for (int j = n - 1; j >= 0; j--) {
int k = temp[j] / (int)pow(radix, i) % radix;
array[--count[k - minR]] = temp[j];
}
}
}
归并排序
利用了分治的思想
- 递归分割序列,从中间将序列一分两半(分割为一个元素时,可以认为这个子序列是有序的)
- 递归合并两个已排序的子序列

void merge(vector<int>& array, vector<int>& temp, int left, int right, int middle) {
if (left >= right) {
return;
}
// 左序列正序,右序列倒序
for (int i = left; i <= middle; i++) {
temp[i] = array[i];
}
for (int i = middle + 1; i <= right; i++) {
temp[right - (i - middle) + 1] = array[i];
}
// 左右子序列索引
int index1 = left;
int index2 = right;
// 合并后的索引
int index = left;
// 从左右序列两边向中间的方向,归并
while (index <= right) {
if (temp[index1] <= temp[index2]) {
array[index++] = temp[index1++];
} else {
array[index++] = temp[index2--];
}
}
}
void MergeSort(vector<int>& array, vector<int>& temp, int left, int right) {
if (left >= right) {
return;
}
int middle = (right - left) / 2 + left;
MergeSort(array, temp, left, middle);
MergeSort(array, temp, middle + 1, right);
merge(array, temp, left, right, middle);
}
R.Sedgewick优化的两路归并,减少了判断的次数
索引排序
没什么好说的,就是为了减少数组中的赋值次数的优化方法。shell排序和堆排序不适用,会增加时间消耗。
第一种,索引序列IndexArray[i]存放原数组Array[i]中的数据索引,排序后,排序后的数组Array[i]对应Array[IndexArray[i]]

第二种,索引序列IndexArray[i]存放原数组Array[i]中的数据索引,排序后,排序后的数组Array[IndexArray[i]]对应Array[i]

比较分析
复杂度
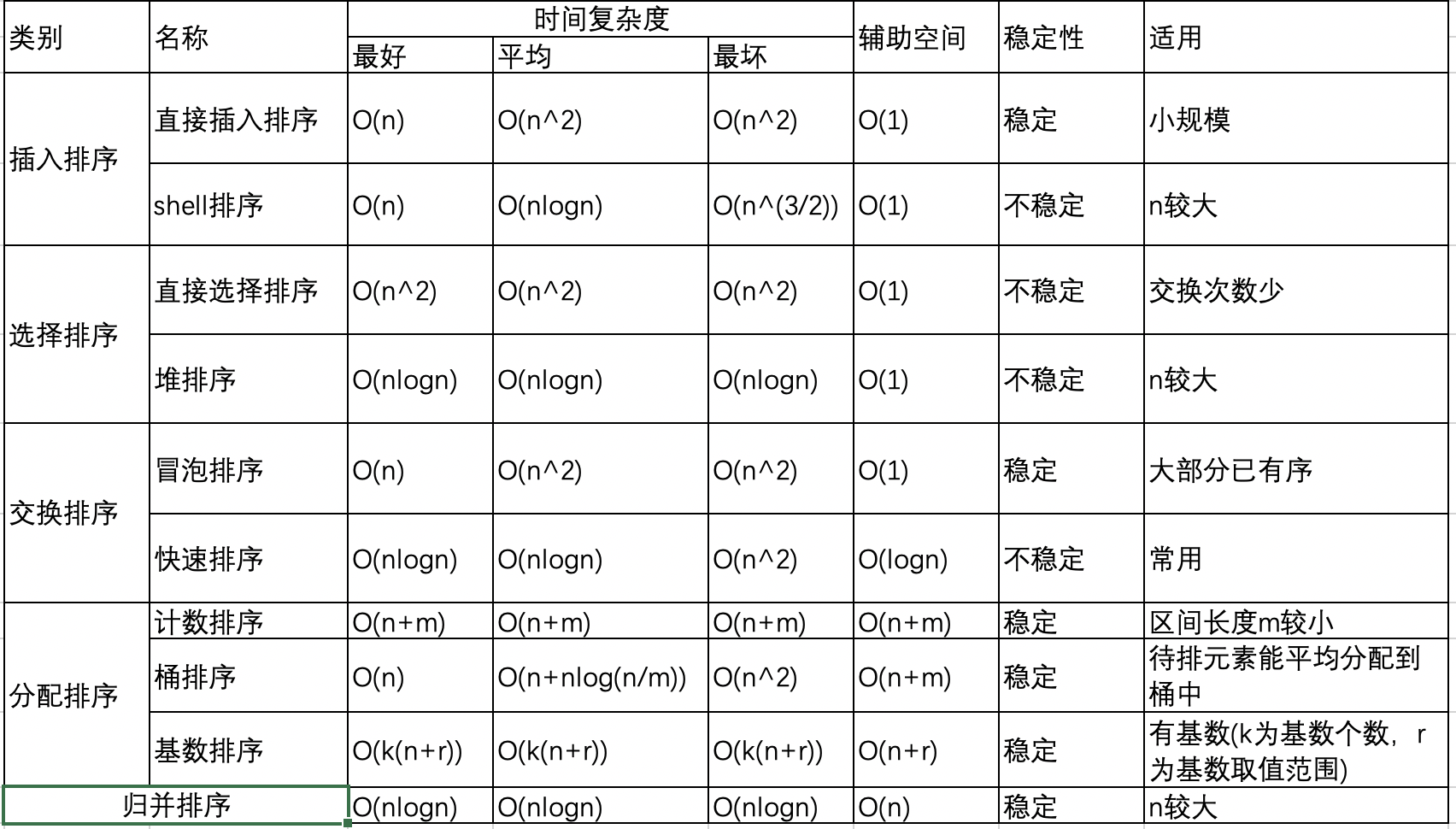
交换与比较
- 直接插入排序
- 最好:$n-1$ 次比较,$2(n-1)$ 次数组赋值
- 最差:$\frac{n(n-1)}{2}$ 次比较,$\frac{(n+2)(n-1)}{2}$ 次数组赋值
- 直接选择排序
- 最好:$\frac{n(n-1)}{2}$ 次比较
- 最差:$\frac{n(n-1)}{2}$ 次比较,$n-1$ 次交换
- 冒泡排序
- 最好:$n-1$ 次比较
- 最差:$\frac{n(n-1)}{2}$ 次比较和交换
REFERENCE
[1]插入排序 - 北京大学[EB/OL]. Coursera.
[2]选择排序 - 北京大学[EB/OL]. Coursera.
[3]交换排序 - 北京大学[EB/OL]. Coursera.
[4]分配排序 - 北京大学[EB/OL]. Coursera.
[5]索引排序 - 北京大学[EB/OL]. Coursera.
[6]算法性能分析 - 北京大学[EB/OL]. Coursera.
文档信息
- 本文作者:wzx
- 本文链接:https://masterwangzx.com/2019/11/26/inner-sort/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)