WZX's Blog

大数据日知录学习(四)：常用数据结构

2020/09/05 大数据理论与架构 共 4676 字，约 14 分钟

简要介绍大数据常用的数据结构

BitMap

位图

将具体数据映射到比特数组中，0表示数据不存在，1表示数据存在。适用于大量数据查询和去重的场景，具有比较高的空间利用率。但是具有以下缺点

  • 数据碰撞。具体数据映射到比特数组中会有碰撞的问题，可以考虑用 Bloom Filter 来解决，Bloom Filter 使用多个 Hash 函数来减少冲突的概率

  • 数据稀疏。稀疏数据的存储会有很大的空间浪费，通过引入 Roaring BitMap 来解决

Roaring Bitmap

将具体数据映射到32位无符号整数按照高16位分桶，低16位放入container中。Roaring Bitmap是对BitMap的改进，通过三种不同的container解决了稀疏数据存储的问题。

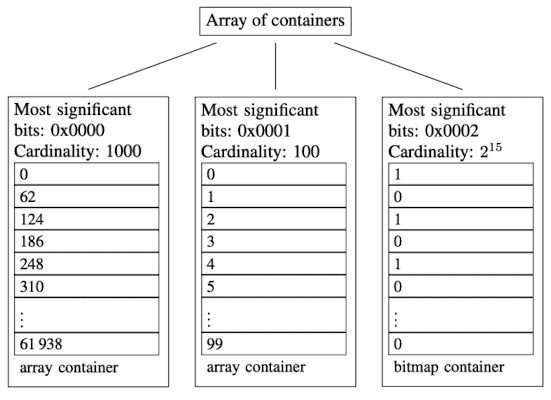
图中示出了三个container

  • 高16位为0000H的ArrayContainer，存储有前1000个62的倍数
  • 高16位为0001H的ArrayContainer，存储有$[2^{16},2^{16}+100)$区间内的100个数
  • 高16位为0002H的RunContainer，存储有$[2\times2^{16},3\times2^{16})$区间内的所有偶数，共$2^{15}$

ArrayContainer

当桶内数据的基数不大于4096时，会采用它来存储，其本质上是一个无符号短整型的 有序数组。数组初始长度为4，随着数据的增多会自动扩容至最大长度4096

BitMapContainer

当桶内数据的基数大于4096时，会采用它来存储，其本质就是长度为1024的无符号长整型数组表示的BitMap。

复杂度分析

在创建一个新container时，如果只插入一个元素，默认会用ArrayContainer来存储。当ArrayContainer的容量超过4096后，会自动转成 BitMapContainer存储。低于4096时Arraycontainer比较省空间，高于4096时BitMapContainer比t较省空间。即ArrayContainer存储稀疏数据，Bitmapcontainer适合存储稠密数据，可以最大限度地避免内存浪费。

增删改查的时间复杂度方面，BitMapContainer只涉及到位运算，复杂度为O(1)。而ArrayContainer需要用二分查找在有序数组中定位元素故为O(logN)。空间占用方面，BitMapcontainer恒定为8192B，而ArrayContainers的空间占用与序列基数有关 。

Hyperloglog

基于$n$重伯努利实验原理的不精准去重统计。假设一直抛硬币，直到它出现正面为止，记为一次伯努利实验。对于$n$重伯努利实验，每此伯努利实验的抛掷次数为$k_1,k_2,\cdots,k_n$，最大抛掷次数为$k_{max}$。由极大似然估计可知，$n=2^{k_{max}}$。假设一共有$m$轮$n$重伯努利实验，随着$m$的增加，使用最大抛掷次数的调和平均数，会使极大似然估计值与越来越接近真实值。

对于具体数据通过哈希函数映射成比特串，根据比特串的高几位进行分桶，每个桶相当于一轮$n$重伯努利实验。从右往左看，比特串首次出现1的位置即为当前伯努利实验的抛掷次数$k$，每次插入数据都将更新对应桶中的$k_{max}$。根据极大似然估计和调和平均值，即可最终计算出所有轮的总实验次数$m\times n$，可用以下公式计算，其中$const$为修正常数随着$m$而变化

\[DV_{HLL}=const\times m\times \frac{m}{\sum^m_{j=1}\frac{1}{2^{R_j}}}\]
  • 由于哈希函数的存在，重复的数据不会进行统计
  • 所有数据都被均等的分在$m$个桶中，每个桶中有$n$个元素
  • 使用调和平均数替换平均数，不容易受到大数值的影响

Bloom Filter

布隆过滤器

二进制向量结构(空间利用率和时间效率)，检测集合中是否存在某元素，存在误判但不存在漏判

原理

长度为m的位数组存储集合信息，使用k个独立的哈希函数将数据映射到位数组空间。

# 集合A初始化布隆过滤器
BloomFilter(set A, hash_functions, integer m)
    # 位数组
    filter [1...m] = 0
    foreach a_i in A:
        foreach h_j in hash_functions:
            filter[h_j(a_i)] = 1
        end foreach
    end foreach

    return filter

元素a，若对于相同的k个哈希函数，对应位都为1，则存在于集合中

MembershipTest(element, filter, hash_functions)
    foreach h_j in hash_functions:
        if filter[h_i(element)] != 1 then
            return false
    end foreach

    return true

误判率

对于集合大小n, 哈希函数个数k, 位数组大小m，误判率为 $p_{fp}\approx (1-e^{-kn/m})^k$ ，最优的哈希函数个数为 $k=\frac{m}{n} ln2$ ，故已知集合大小 $n$ 的情况下，并且在期望的误判率 $P$ 下，位数组的大小为 $m=-\frac{nlnp}{(ln2)^2}$

改进

计数BF，位数组的一个比特位拓展为多个比特位，就可以增加删除集合成员的功能

SkipList

可替代平衡树的数据结构，依靠随机数保持数据的平衡分布。在最坏情况下效率要低于平衡树，在大多数情况下仍然非常搞笑。增删改查的时间复杂度都是O(logn)。

在有序链表的基础上，以随机概率给部分结点增加指针，指向更远的后方结点。如图所示，结点的层数对应着指针的个数。

查找

search(list, searchKey)
	x = list.head
	# 从当前层数遍历到最底层
	for i in [list.level, 1]:
		# 每层找到第一个大于或等于key的前一个结点
		while x.next[i].key < searchKey:
			x = x.next[i]
	# 底层的后一个结点即是目标值
	x = x.next[1]
	if x.key == searchKey: return x.val
	else: return failure

插入&更新

以下是随机生成层数的伪代码

randomLevel()
	level = 1
	# random() 生成[0, 1)的随机数
	# 以p的概率依次增加层数
	while random() < p and level < maxLevel:
		level += 1
	return level

以下是插入的伪代码

insert(list, searchKey, newValue)
	update = array[maxLevel]
	x = list.head
	# 从当前层数遍历到最底层
	for i in [list.lever, 1]:
		# 每层找到第一个大于或等于key的前一个结点
		while x.next[i].key < searchKey:
			x = x.next[i]
		update[i] = x
	x = x.next[1]
	# 更新
	if x.key == searchKey: x.val = newValue
	else:
		level = randomLevel
		if level > list.level:
			# 新结点大于当前层数，则要添加新层head
			for i in [list.level + 1, level]:
				update[i] = list.head
			list.level = level
		# 由下往上插入结点 update[i] -> x -> update[i].next[i]
		x = node(level, searchKey, newValue)
		for i in [1, level]:
			x.next[i] = update[i].next[i]
			update[i].next[i] = x

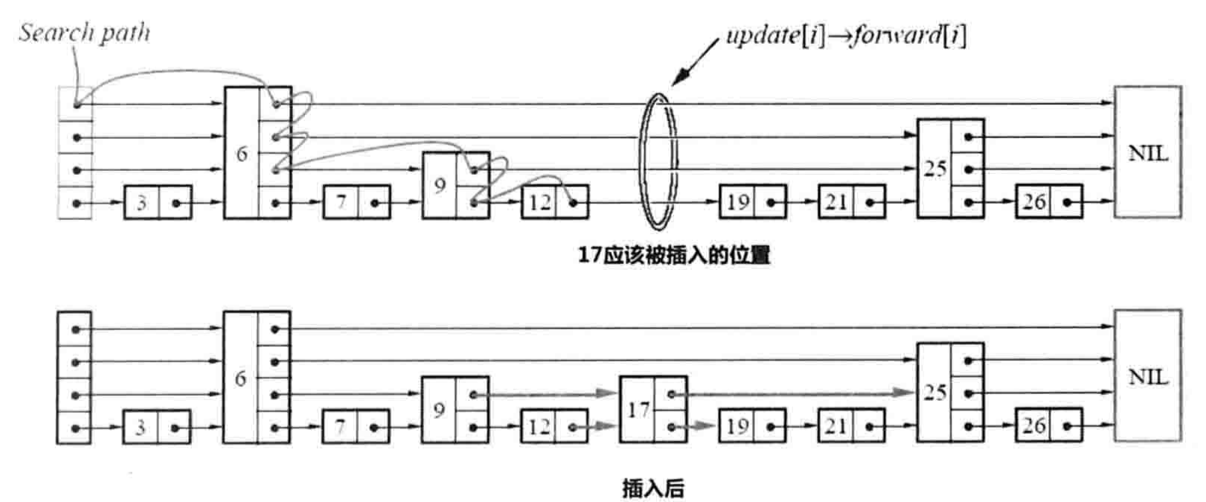
下图所示插入17的过程

删除

删除的过程与插入类似

delete(list, searchKey)
	update = array[maxLevel]
	x = list.head
	# 从当前层数遍历到最底层
	for i in [list.lever, 1]:
		# 每层找到第一个大于或等于key的前一个结点
		while x.next[i].key < searchKey:
			x = x.next[i]
		update[i] = x
	# 找到要删除的结点
	x = x.next[1]
	if x.key == searchKey:
		for i in [1, list.level]:
			# 要删除的结点在当前层没有，在更高的层也不会有
			if update[i].next[i] != x: break
			update[i].next[i] = x.next[i]
		# 更新当前的层数
		while list.level > 1 and list.head.next[list.level] == null:
			list.level -= 1

LSM

Log-structured Merge-tree

将大量随机写转化为批量的顺序写，提升磁盘写入速度，牺牲了读性能，读性能可以使用布隆过滤器进行优化。

以LevelDB为例

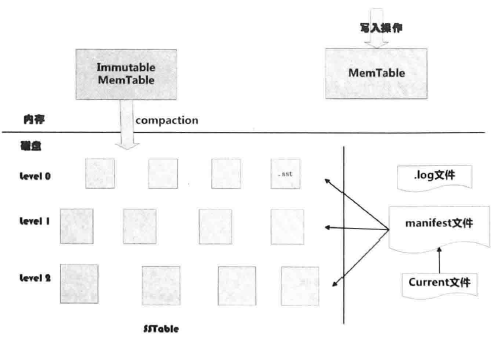
存储结构

内存中的MemTable和磁盘上的各级SSTable文件就形成了LSM树

  • 内存
    • MemTable：跳表结构。用于数据的快速插入
    • Immutable MemTable：只读的跳表结构。在MemTable占用内存达到一定阈值之后，便转化为Immutable MemTable
  • 硬盘

    • Current：当前manifest文件名

    • Manifest：SSTable的元信息，各层级SSTable文件的Level，文件名，最大最小key

    • Log：MemTable的插入日志。用于系统崩溃，内存中的MemTable数据丢失后的数据恢复

    • SSTable：Immutable MemTable导出到磁盘的结果。层级key有序文件结构。第0层有minor compaction生成会出现key重叠现象，但其余层的文件里不会存在key重叠现象

compaction

  • minor compaction: 当MemTable达到一定大小时，转化为Immutable MemTable并按顺序写入level0的新SSTable文件中。不处理删除操作

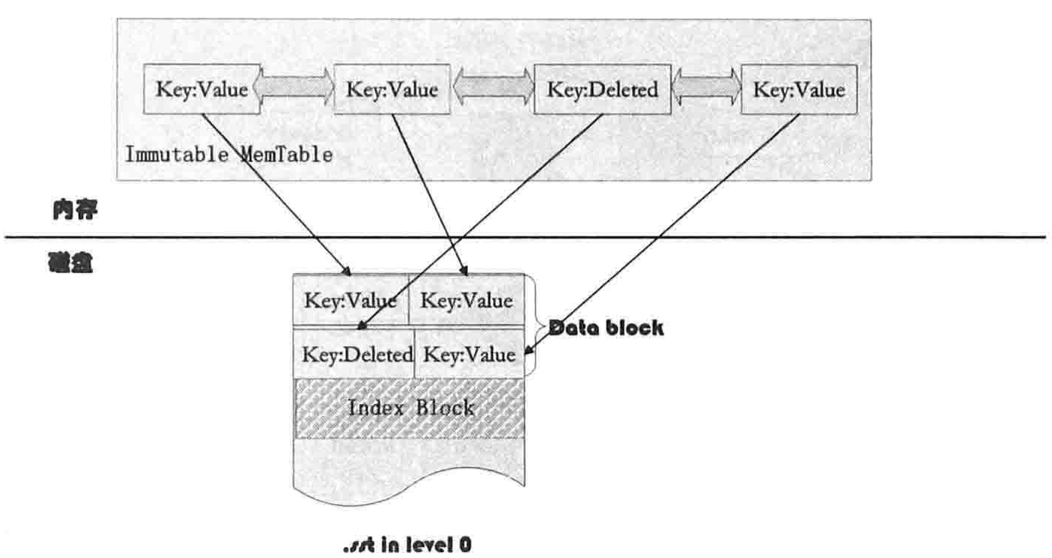
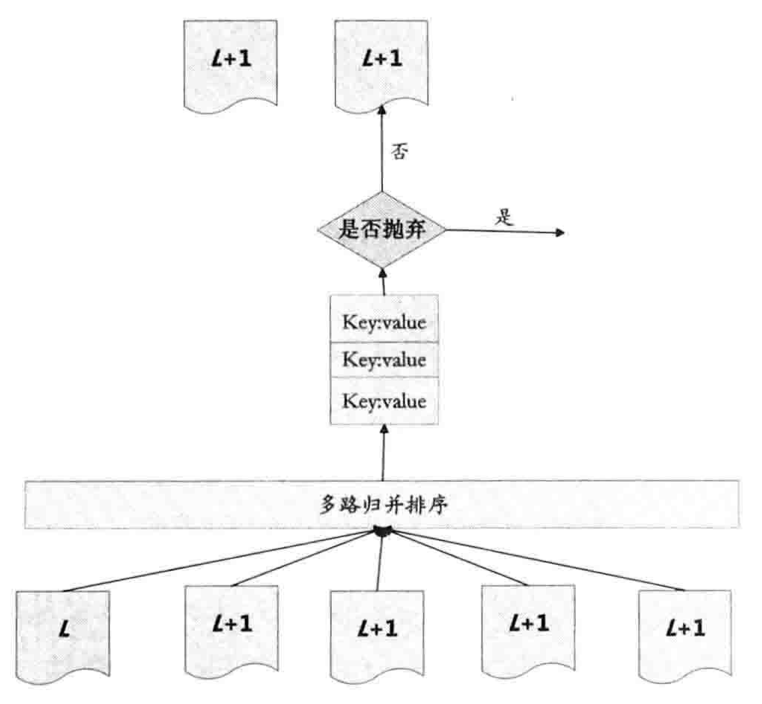
  • major compaction: 当某个Level下的SSTable文件数目超过一定数量时，从这个Level中选择一个文件(Level0 需要选择所有key重叠的文件)和高一Level的文件合并。

    • 轮流选择Level层的文件
    • Level+1层选择和Level层文件在key range上有重叠的所有文件进行合并
    • 使用多路归并排序，并判断这个KV是否被删除，形成一系列新Level+1层的多个文件
    • 删除Level层的那个文件和旧Level+1层的所有文件

Merkle Hash Tree

主要用于海量数据下快速定位少量变化的数据内容，在BitTorrent，Git，比特币等中得到了应用。

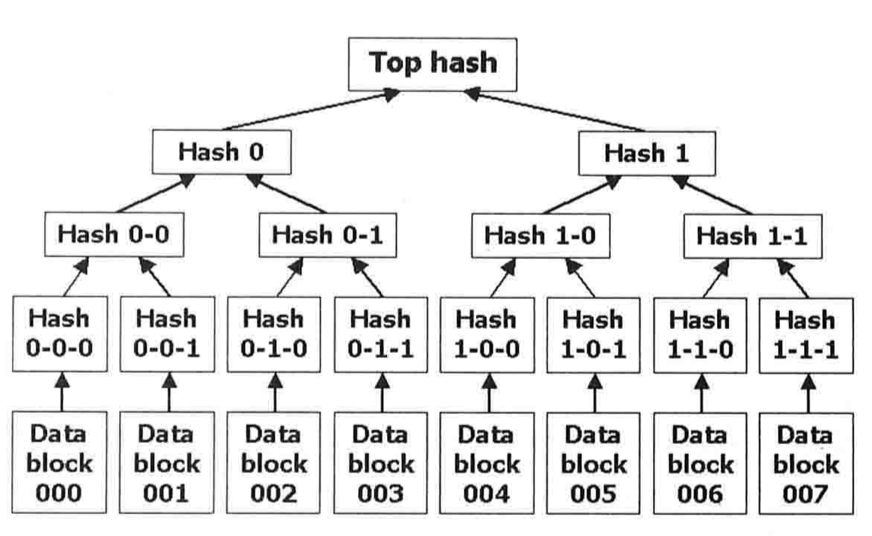
如图所示，叶子结点是每个数据项的哈希值，分支结点则保存其所有子结点的哈希值，依次由下往上推，根结点保存整棵树的哈希值。当某个数据项发生变化时，其对应的叶子结点的哈希值也会发生变化，其祖先结点也会跟着变化，这样在O(logn)时间内就能快速定位变化的数据内容。

REFERENCE

  1. 大数据日知录
  2. 高效压缩位图RoaringBitmap的原理与应用
  3. HyperLogLog 算法的原理讲解以及 Redis 是如何应用它的

文档信息

Search

    Table of Contents