总结常见的字符串匹配算法

RK算法

RK算法全称Rabin-Karp算法，由算法的两位发明者Rabin和Karp的名字来命名。RK算法的核心思想是比较两个字符串的哈希值来判断两个字符串是否完全一样。问题的关键就转化为如何在 $O(1)$ 的时间内生成子串的哈希值并且尽量减少哈希碰撞。简单地，可以使用将字符串每位的ASCII码值相加作为哈希值，在匹配过程中通过减去首部旧字符的ASCII码再加上尾部新字符的ASCII码来达到增量哈希的效果，以在 $O(1)$ 时间内生成哈希值。由于哈希算法可能产生哈希冲突所以性能并不稳定。

下面通过一个例子来解释一下

1. 首先生成模式串的哈希值，2+3+5=10

   

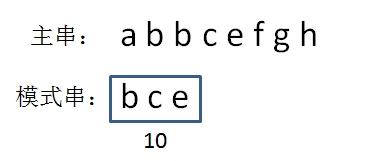
2. 计算主串中第一个等长子串的哈希码，1+2+2=5

   

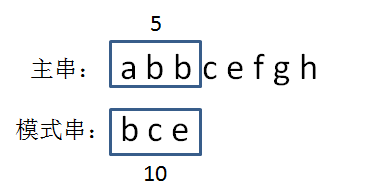
3. 经过比较模式串和第一个子串显然不相同，这时子串后移一位生成新的子串的哈希码。5-1+3=7

   

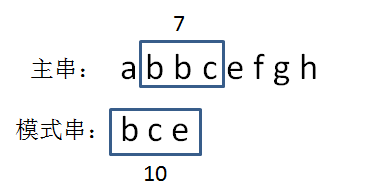
4. 显然也不相同，这时子串后移一位生成新的子串的哈希码。7-2+5=10

   

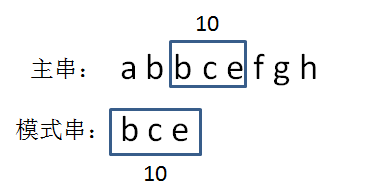
5. 这时哈希值相同，再逐位验证两个字符串是否相同以排除哈希冲突的情况

   

这里是已经实现的代码

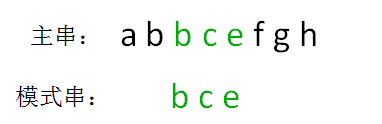
BM算法

BM算法全称Boyer-Moore字符串搜索算法，由算法的两位发明者Bob Boyer和Jstrother Moore的名字来命名。通过后缀比较的方式让模式串尽可能的多移动几位从而减少无谓的字符比较，通过应用以下两种策略实现。好后缀策略和坏字符策略是相互独立的，所以在每轮字符比较后取向后挪动距离最长的那种策略。

坏字符

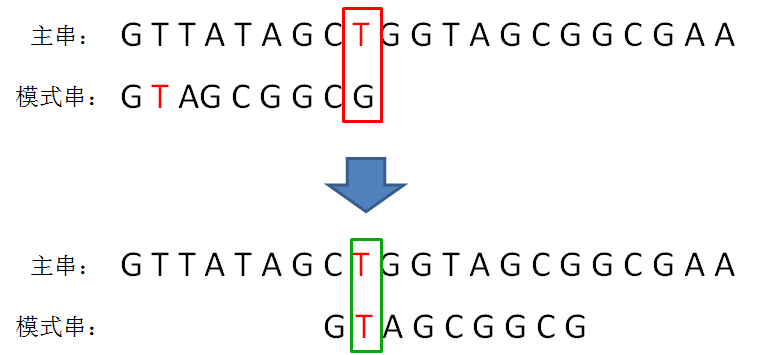
如下图所示，从后往前匹配，当遇到模式串和主串的字符不匹配时，这个字符就是坏字符。从后往前搜索模式串中与坏字符匹配的字符并将此字符与坏字符对齐，这就是下一次可能匹配的位置。因为只有模式串和坏字符匹配，这两个字符串才可能匹配，而从后往前搜索是为了找到挪动跨度最短的下一次需要匹配的位置，防止跳过可能的解。

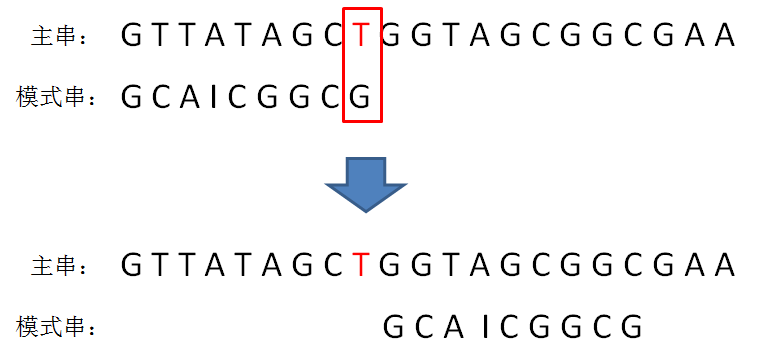
如下图所示，如果坏字符在模式串中不存在，则只能将模式串移动到主串坏字符的下一位

好后缀

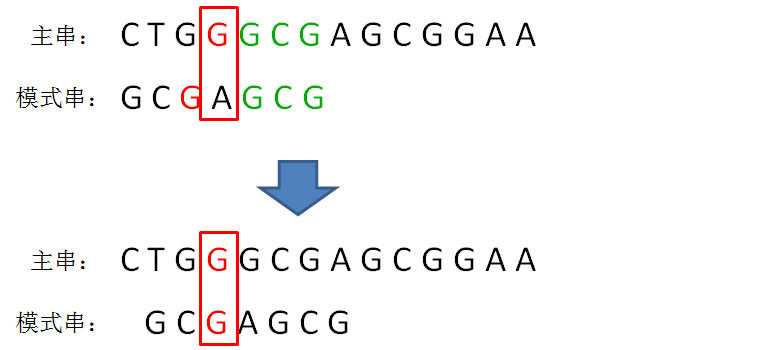
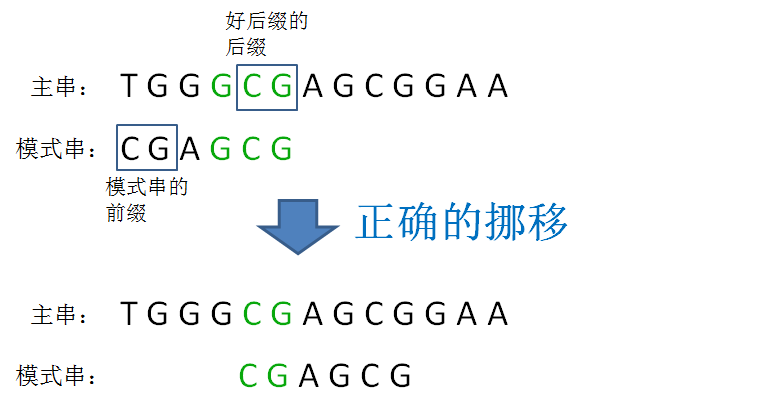
如下两图所示，当找到了模式串和主串的匹配后缀时，这个后缀就是好后缀。从前往后搜索模式串中与好后缀匹配的模式串子串，或者与好后缀的前缀匹配的模式串前缀并对齐，这就是下一次可能匹配的位置。因为只有模式串和好后缀匹配，这两个字符串才可能匹配，而当好后缀的前缀和模式串的前缀匹配时这也是一个可能的匹配位置。

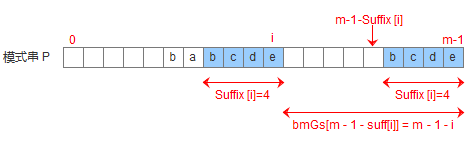
好后缀在实现过程中，如下图所示，可以先构建后缀数组suffix，下标表示与模式串后缀匹配的最大长度，值表示与后缀匹配的子串的结尾索引。

由suffix数组就可以推导出bmGs数组，下标表示好后缀在模式串中的前一个索引，值表示模式串应该后移的距离，可以分为三种情况

• 模式串中有子串匹配上好后缀

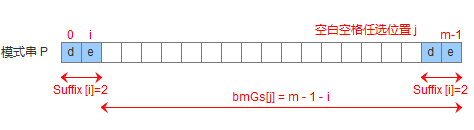
• 模式串中没有子串匹配上好后缀，但找到一个好后缀的前缀匹配的模式串前缀

• 没有任何匹配的子串或者前缀，则后移模式串长度的距离

这里是已经实现的代码

KMP算法

KMP算法全称Knuth-Morris-Pratt算法，由算法的三位发明者D.E.Knuth和J.H.Morris和V.R.Pratt的名字来命名。相对于BM算法，KMP算法专注于已匹配的前缀。

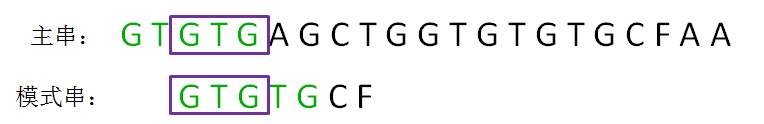
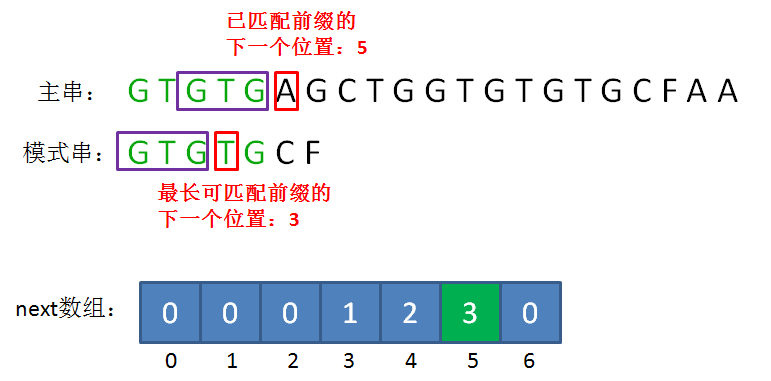
如上两张图所示的这种情况，当模式串和主串的已匹配前缀中出现了最长可匹配后缀子串和最长可匹配前缀子串时，这时直接将两个子串对齐才是下一个可能匹配的位置，这样就将模式串移动了多位从而减少了不必要的字符匹配。由图可知，模式串移动的位置是由模式串和主串的已匹配前缀的长度决定的，所以next数组保存了这两者的对应关系。

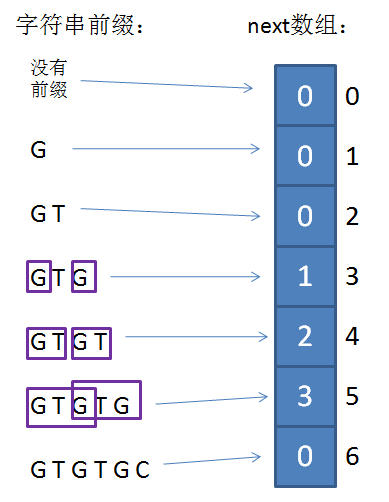
如下第一张图所示，数组的下标代表了已匹配前缀的下一个位置，元素的值则是最长可匹配前缀子串的下一个位置。如下第二张图所示，当遇到前缀不匹配时，则根据已匹配前缀的下一个位置从next数组中取出最长可匹配前缀的下一个位置，将这个位置与已匹配前缀的下一个位置继续对比，这就相当于将模式串后移到了匹配前缀的位置继续比较。这个过程可以迭代，具体理由可以参考下文next数组的推导进行思考。

由next数组的含义可知，仅由模式串即可生成next数组。如果使用暴力法生成需要 $O(n^2)$ 的时间，这显然是低效的，可以使用动态规划的方法去优化。动态规划最不好想的就是递推公式。可以假设两个变量i(当前next数组的下标即已匹配前缀的下一个位置)和j(最长可匹配前缀子串的下一个位置)。在递推时会遇到两种情况。

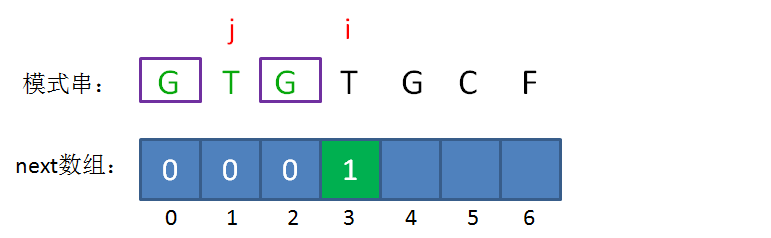
如下图所示，如果next[i-1]==next[j]，这说明已匹配前缀的最后一个字符与最长可匹配前缀子串的下一个字符一致，那么最长可匹配前缀子串长度就会增加1，即最长可匹配前缀子串的下一个位置也会后移一位，即next[i]=++j。

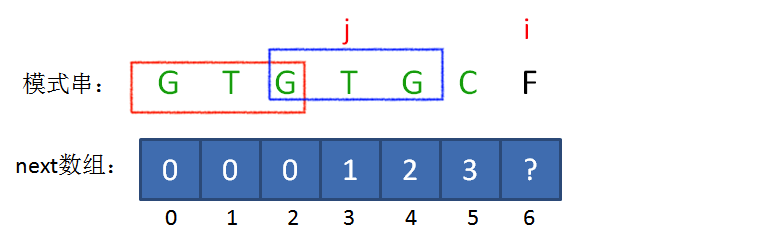
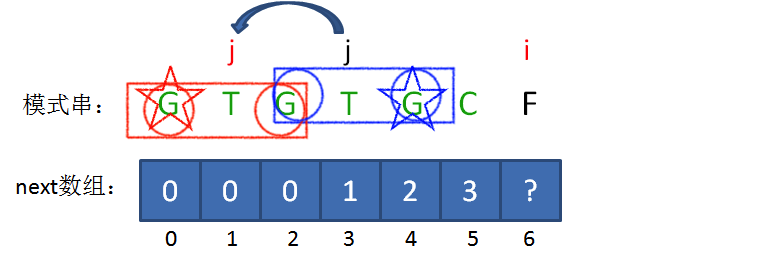
如果next[i-1]!=next[j]，情况就比较复杂。如下第一张图所示，当前的最长匹配前缀即next[i-1]不能保证继续匹配，那么应该更换前缀为比最长匹配前缀稍短一点的前缀继续匹配。如下第二张图所示，我们需要找到红框的前缀和蓝框的后缀中的最长部分(除原最长匹配前缀之外)，next[j]的含义表示红框中的最长匹配前缀，对应的蓝框中的最长匹配前缀也应相同，如图红蓝圆圈表示的区域，我们可以推导出 $red_{prefix}=red_{suffix}=blue_{prefix}=blue_{suffix}\Rightarrow red_{prefix}=blue_{suffix}$ ，所以我们已经找到了下一次应该更换的前缀，如图红蓝星型表示的区域，此时再进行对比即可。

这里是已经实现的代码

REFERERENCE

1. 漫画：什么是字符串匹配算法？—— 程序员小灰
2. 漫画：如何优化字符串匹配算法？—— 程序员小灰
3. 漫画：什么是KMP算法？—— 程序员小灰
4. Boyer-Moore高质量实现代码详解与算法详解——苯苯的小木屋