深层神经网络其实与 浅层神经网络 类似,只是含有多个隐藏层,可以实现更复杂的功能
符号约定
- \(m\) :表示样本的个数
- \((t)_{a\times b}\) :矩阵 t 的形状
- \(t^{[l]}\) :表示第 l 层(第0层即输入层)的参数 t
- \(n^{[l]}\) :表示第 l 层的节点个数
- \(t^{(i)}\) : 表示第 i 个样本的参数 t
- \(\hat{y}\) :表示预测值
- \(a^{[l]}\) :表示第 l 层的节点的输出值
- \(g^{[l]}(z^{[l]})\) :表示第 l 层的激活函数
正向传播
正向传播的实现比较简单,其实就是对 浅层神经网络的正向传播 的推广,寻求更一般化的公式
原理
逐层向后传播,由前一层的输出值 \(a^{[l-1]}\) 计算出当前层的输出值 \(a^{[l]}\)。并保存当前层的 \(z^{[l]}\) ,这用于反向传播的计算
公式
这里直接给出矩阵化后的公式,具体推导过程可以类比 浅层神经网络的正向传播
\[(Z^{[l]})_{n^{[l]}\times m}=(W^{[l]})_{n^{[l]}\times n^{[l-1]}}\cdot (A^{[l-1]})_{n^{[l-1]}\times m}+b^{[l]} \\ A^{[l]}=g^{[l]}(Z^{[l]})\]反向传播
这里的成本函数采用交叉熵成本函数
原理
逐层向前传播,由当前层的偏导数 \(\frac{\partial{L}}{\partial{a^{[l]}}}\) 计算出前一层的偏导数 \(\frac{\partial{L}}{\partial{a^{[l-1]}}}\) ,并计算出当前层对参数 w,b 的偏导数 \(\frac{\partial{J}}{\partial{w^{[l]}}}、\frac{\partial{J}}{\partial{b^{[l]}}}\) ,再对参数 w,b 进行更新
公式
这里直接给出矩阵化后的公式,具体推导过程可以类比 浅层神经网络的反向传播
\[(\frac{\partial{L}}{\partial{Z^{[l]}}})_{n^{[l]}\times m}=\frac{\partial{L}}{\partial{A^{[l]}}} * (g^{[l]})'(Z^{[l]}) \\ (\frac{\partial{L}}{\partial{A^{[l-1]}}})_{n^{[l-1]}\times m}=((W^{[l]})_{n^{[l]}\times n^{[l-1]}})^{T}\cdot (\frac{\partial{L}}{\partial{Z^{[l]}}})_{n^{[l]}\times m} \\ \frac{\partial J}{\partial W^{[l]}}=\frac{1}{m} \cdot \frac{\partial L}{\partial Z^{[l]}} \cdot A^{[l-1]T} \\ \frac{\partial J}{\partial b^{[l]}}=\frac{1}{m}sum(\frac{\partial L}{\partial Z^{[l]}},axis=1)\]这里稍微解释一下第二个式子
假设 L 为损失函数(关于 \(z_{1},z_{2},\cdots ,z_{n_{0}}\) 的函数),z 代表当前层的值,a 代表前一层的输出值,并且当前层有 \(n_{0}\) 个节点,前一层 \(n_{1}\) 有个节点
总结
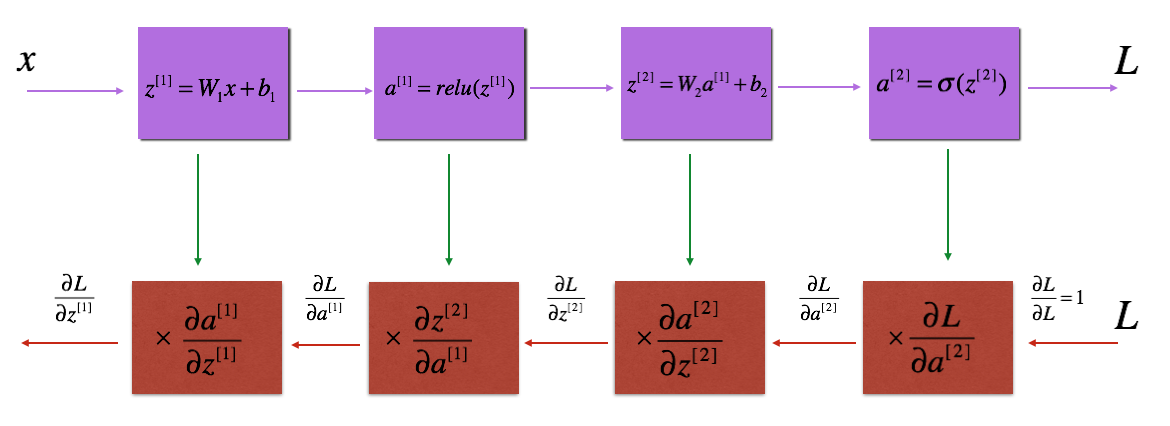
demo
文档信息
- 本文作者:wzx
- 本文链接:https://masterwangzx.com/2018/12/15/deep-neural-network/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)