WZX's Blog

梯度下降的优化算法

2018/12/21 MachineLearning 共 3221 字，约 10 分钟

随着训练样本数量的提升，我们训练后的模型的表现也越来越好，但每次迭代的时间也不断增加。我们主要通过，减少完成一次参数更新的样本数量，以及利用算法尽量从最短路径更新参数，来优化梯度下降算法

MBGD SGD BGD

  • Batch Gradient Descent，即批量梯度下降法。每次迭代将所有数据用于计算梯度，并更新参数。这个做法优点与缺点显而易见。优点就是样本数量多，样本噪声小，成本函数的下降曲线会比较平滑，最终我们的模型可能会更好。缺点就是每次迭代的时间太长，会受内存限制，同时也不能在训练过程中增加训练样本。但在数据量比较小的情况下，我觉得批量梯度下降法表现得很好

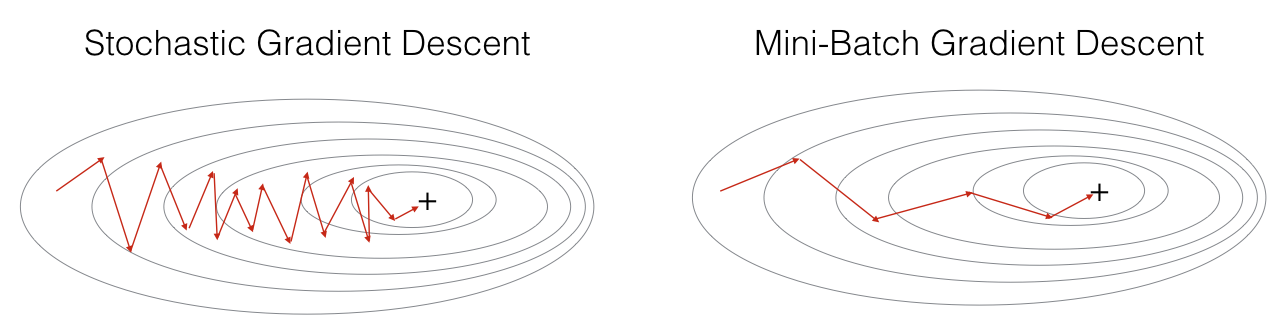
  • Stochastic Gradient Descent，即随机梯度下降法。这个其实相当于 MBGD 中 batch 为1的情况，即每次只迭代一个训练样本。虽然不是每次迭代得到的成本函数都向着全局最优方向，但是大的方向是逐渐趋向全局最优解的，最终的结果往往是在全局最优解附近，并在周围徘徊

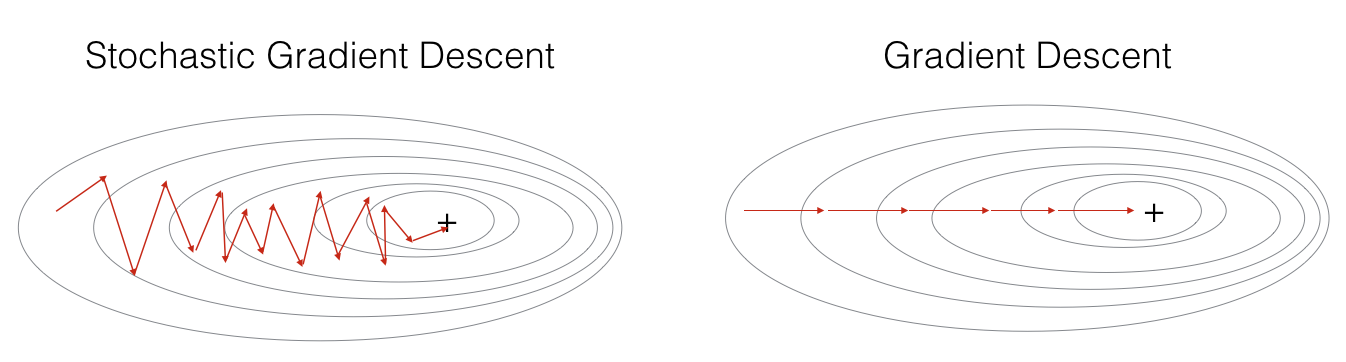
  • Mini-batch Gradient Descent，即小批量批梯度下降法。这个算法有一个超参数 batch。将训练样本分成许多小份，每份的大小就是 batch。每次正向和反向传播时，就对这些样本进行迭代。每对所有训练样本完成一次迭代，则称为一个 Epoch。MBGD 大幅降低了每次迭代的时间。虽然每次迭代的样本并不是全部样本，数据存在噪声，所以成本函数的下降曲线会有些波动，但总体趋势依然是下降的

Momentum Gradient Descent

在大多数情况下，成本函数的图像不是那么规则，梯度下降可能会走很多“弯路”。如果使用 MBGD 或 SGD ，那梯度下降的方向则会更加波动

指数加权平均

原理

当我们要计算一组数的平均值时，通常做法是将这些数求和并且除以个数，但如果数据量比较大且计算次数比较多的时候，这样的计算就占用较多资源。指数加权平均 本质是以指数式递减加权的移动平均。通过递推的形式，各数值的加权随时间而指数式递减，越近期的数据加权越重，但较旧的数据也给予一定的加权。通过调整超参数 $\beta$ 的值，可以调整对历史数据的权重

  • $V_t$ ： 当前指数加权平均值
  • $\theta_t$ ： 当前数据值
\[\begin{equation} \begin{aligned} V_0&=0 \\V_1&=\beta V_{0}+(1-\beta)\theta_1 \\V_2&=\beta V_{1}+(1-\beta)\theta_2 \\ &\cdots \\V_t&=\beta V_{t-1}+(1-\beta)\theta_t \end{aligned} \end{equation}\]

偏差修正

大家可能会发现，因为 $V_0$ 的值为0，这对最初的一些平均值产生比较大的影响，为了消除这个影响，我们对公式做一些修改

\[V_t^{corrected}=\frac{V_t}{1-\beta^t}=\frac{\beta V_{t-1}+(1-\beta)\theta_t}{1-\beta^t}\]

随着 t 的增大，偏差修正项的值越来越接近 1 ，所以该偏差修正项对数据前期影响大，后期影响小

原理

动量梯度下降利用指数加权平均，综合了历史的梯度以平滑本次更新的梯度。每次更新的梯度将不是独立的情况，而是拥有一定权重的历史梯度。如下图所示，红色显示了历史的梯度下降的方向均值，蓝色表示原始梯度方向，红色箭头为合成的方向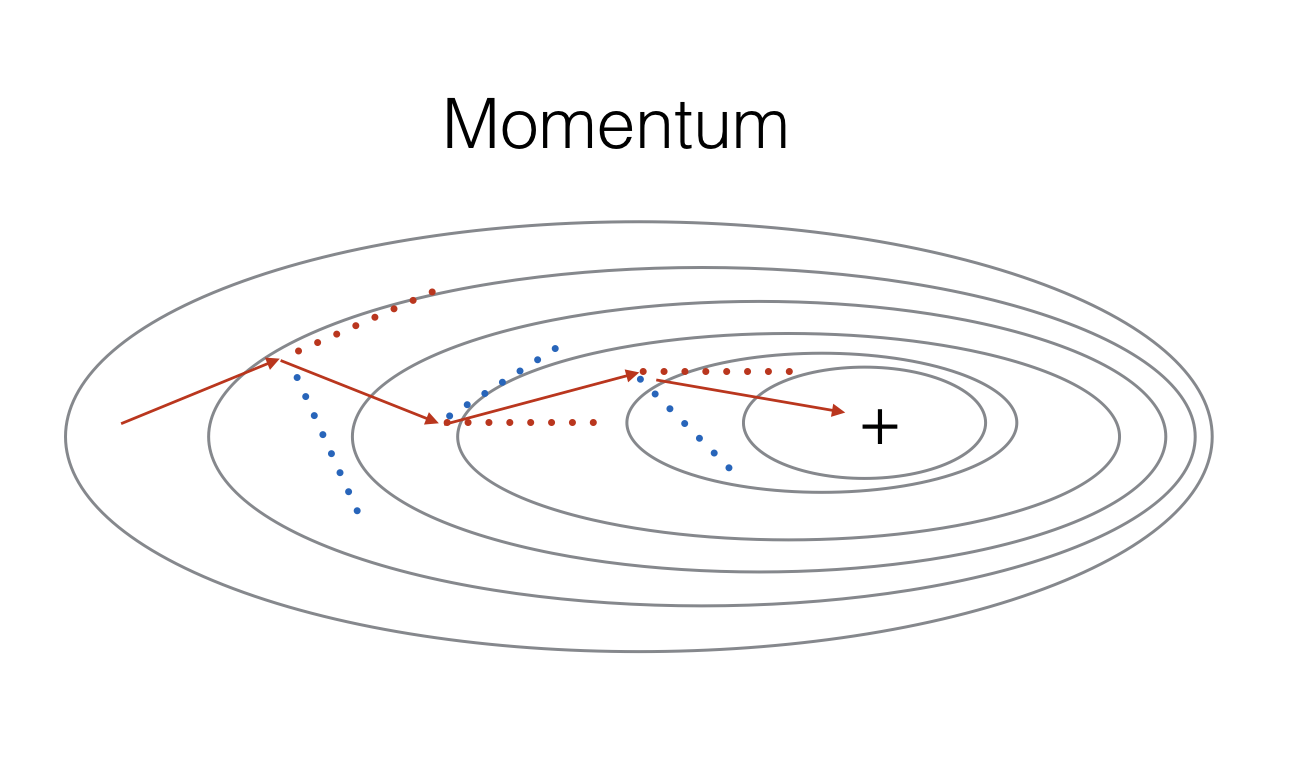

实现

相对梯度下降来说，在参数更新以及梯度计算时有所不同，为了简洁，将 $\frac{\partial{J}}{\partial{W^{[l]}}}$ 简写为 $dW^{[l]}$

\[\begin{equation} \begin{cases} V_{dW^{[l]}}=\beta V_{dW^{[l-1]}}+(1-\beta)dW^{[l]} \\ W^{[l]}:=W^{[l]}-\alpha V_{dW^{[l]}} \end{cases} \\ \begin{cases} V_{db^{[l]}}=\beta V_{db^{[l-1]}}+(1-\beta)db^{[l]} \\ b^{[l]}:=b^{[l]}-\alpha V_{db^{[l]}} \end{cases} \end{equation}\]

一般来说 𝛽 从 0.8~0.999 范围内取值。建议取 0.9

RMSprop

原理

通过全局学习率逐参数的除以经过超参数 $\beta$ 控制的历史梯度平方和的平方根，使得每个参数的学习率不同，梯度大的参数学习率会降低。这样就使得参数梯度的平缓方向，取得更大的进步，而陡峭的方向则会变得平缓，从而加快训练速度

实现

为了简洁，将 $\frac{\partial{J}}{\partial{W^{[l]}}}$ 简写为 $dW^{[l]}$

\[\begin{equation} \begin{cases} S_{dW^{[l]}}=\beta S_{dW^{[l-1]}}+(1-\beta)(dW^{[l]})^2 \\ W^{[l]}:=W^{[l]}-\frac{\alpha}{\sqrt{S_{dW^{[l]}}}+\epsilon}dW^{[l]} \end{cases} \\ \begin{cases} S_{db^{[l]}}=\beta S_{db^{[l-1]}}+(1-\beta)(db^{[l]})^2 \\ b^{[l]}:=b^{[l]}-\frac{\alpha}{\sqrt{S_{db^{[l]}}}+\epsilon}db^{[l]} \end{cases} \end{equation}\]

$\epsilon$ 为一个很小的值，为了防止出现分母为 0 的情况，一般取值为 $10^{-8}$ 。$\beta$ 一般取 0.999

Adam

Adaptive Moment Estimation，自适应矩估计综合了 Momentum Gradient Descent 与 RMSprop，与两者结合体类似，这里直接给出公式，为了简洁，将 $\frac{\partial{J}}{\partial{W^{[l]}}}$ 简写为 $dW^{[l]}$

\[\begin{equation} \begin{cases} V_{dW^{[l]}}=\beta_1 V_{dW^{[l-1]}}+(1-\beta_1)dW^{[l]} \\ V_{dW^{[l]}}^{corrected}=\frac{V_{dW^{[l]}}}{1-(\beta_1)^t} \\ S_{dW^{[l]}}=\beta_2 S_{dW^{[l-1]}}+(1-\beta_2)(dW^{[l]})^2 \\ S_{dW^{[l]}}^{corrected}=\frac{S_{dW^{[l]}}}{1-(\beta_2)^t} \\ W^{[l]}:=W^{[l]}-\frac{\alpha}{\sqrt{S^{corrected}_{dW^{[l]}}}+\epsilon} \end{cases} \\ \begin{cases} V_{db^{[l]}}=\beta_1 V_{db^{[l-1]}}+(1-\beta_1)db^{[l]} \\ V_{db^{[l]}}^{corrected}=\frac{V_{db^{[l]}}}{1-(\beta_1)^t} \\ S_{db^{[l]}}=\beta_2 S_{db^{[l-1]}}+(1-\beta_2)(db^{[l]})^2 \\ S_{db^{[l]}}^{corrected}=\frac{S_{db^{[l]}}}{1-(\beta_2)^t} \\ b^{[l]}:=b^{[l]}-\frac{\alpha}{\sqrt{S^{corrected}_{db^{[l]}}}+\epsilon} \end{cases} \end{equation}\]

总结

各种优化算法对比

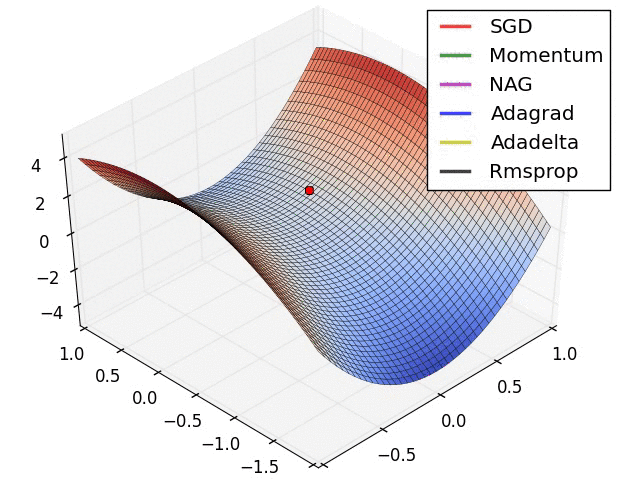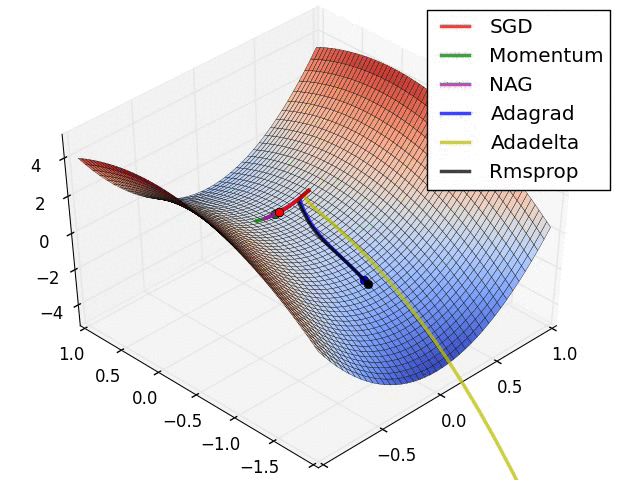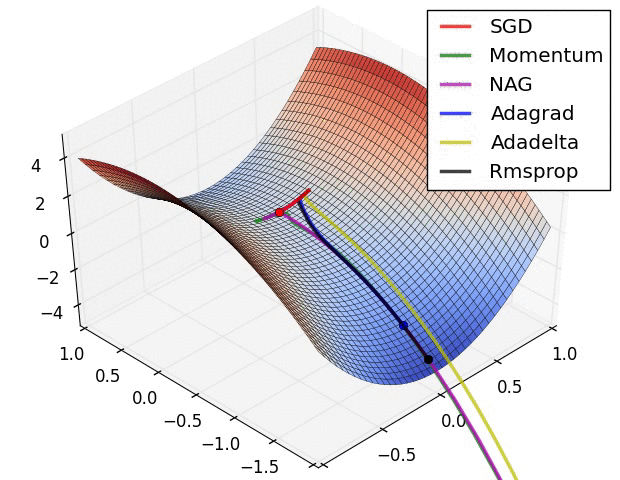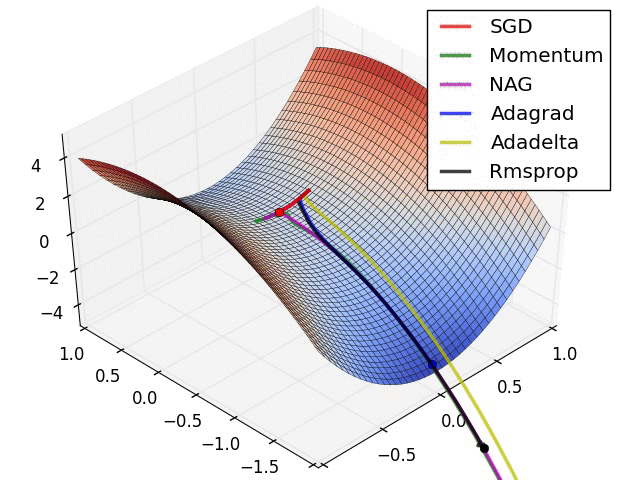
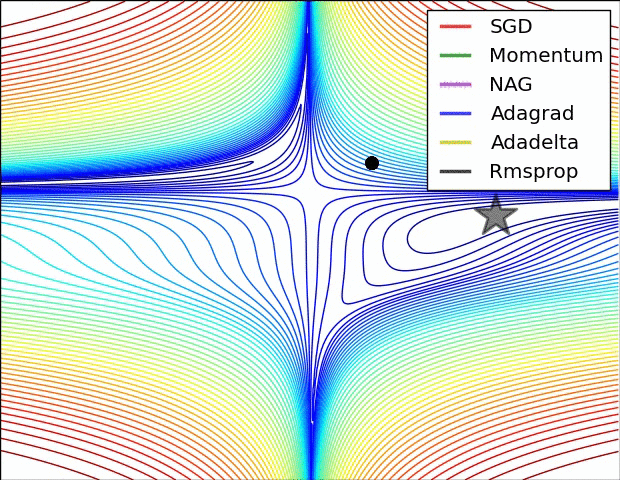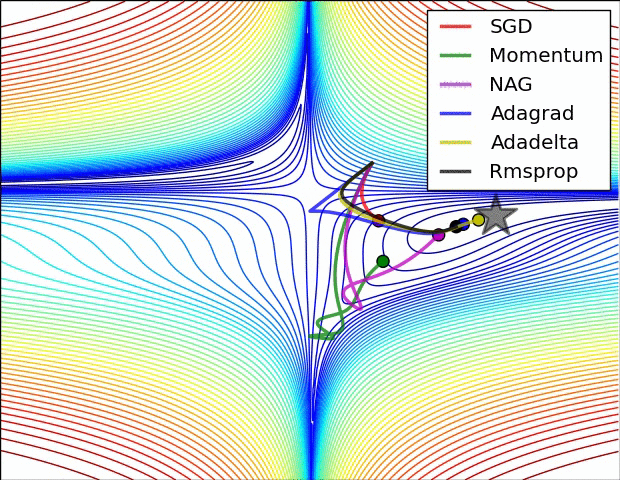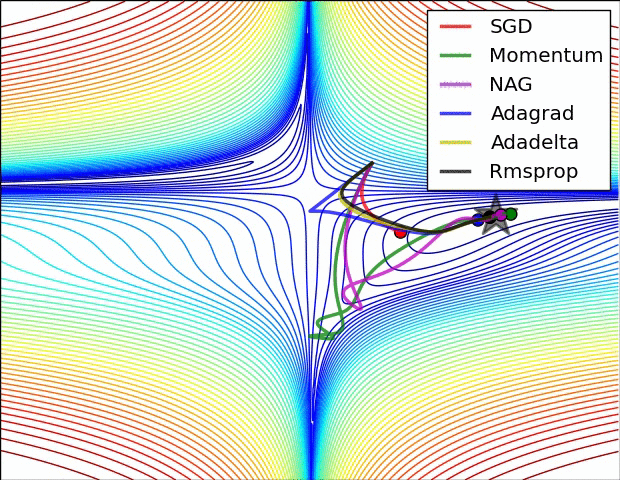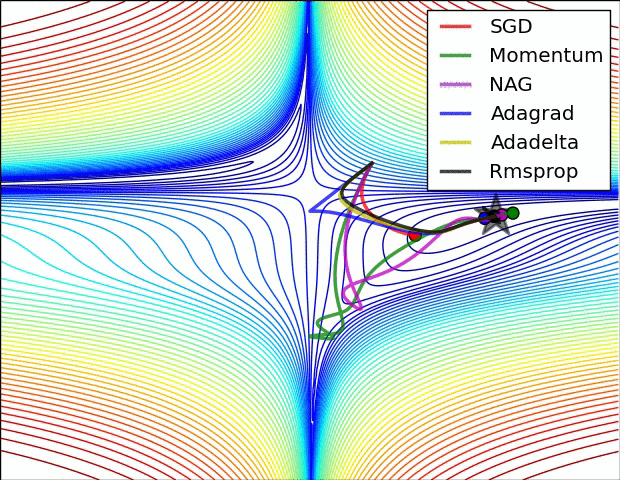
文档信息

Search

    Table of Contents