LeetCode 上的一个题目觉得很有意思
要求
给定一个 n × n 的二维矩阵表示一个图像。
将图像顺时针旋转 90 度。
说明:
你必须在原地旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像
方法一
首先想到的就是找出旋转前后矩阵元素的对应关系,再一一变换
旋转坐标关系式
对于旋转,如果用坐标表示,我们就能很容易获得对应的关系
设 $(x,y)$ 为旋转前的点坐标,$(x’,y’)$ 为旋转后的点坐标
$\alpha$ 为初始位置的夹角,$\beta$ 为旋转角, $r$为点到原点距离
化简得
\[\begin{equation} \left\{ \begin{array}{l} x' = r\cdot cos(\alpha)cos(\beta) - r\cdot sin(\alpha)sin(\beta) \\ y' = r\cdot sin(\alpha)cos(\beta) + r\cdot cos(\alpha)sin(\beta) \\ \end{array} \right. \end{equation}\]带入 $x = r\cdot cos(\alpha) , y = r\cdot sin(\alpha)$ 得
\[\begin{equation} \left\{ \begin{array}{l} x' = x\cdot cos(\beta) – y\cdot sin(\beta) \\ y' = x\cdot sin(\beta) + y\cdot cos(\beta) \\ \end{array} \right. \end{equation}\]我们是顺时针转90度,带入 $\beta=-90$,就得到了旋转前后坐标的对应关系
\[\begin{equation} \left\{ \begin{array}{l} x' = y \\ y' = -x \\ \end{array} \right. \end{equation}\]坐标映射
已知旋转坐标关系式,我们还需找出矩阵的行号,列号与坐标的对应关系,才能得出旋转前后元素行号和列号的对应关系
我们令矩阵在坐标系中的初始位置在第二象限
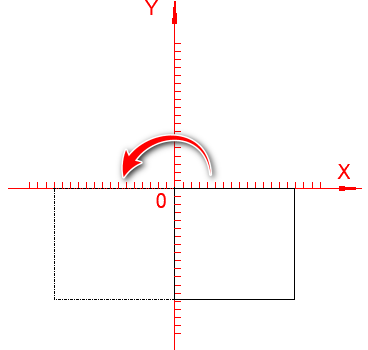
可以找出关系式
\[\begin{equation} \left\{ \begin{array}{l} x = col \\ y = -row \\ \end{array} \right. , \left\{ \begin{array}{l} x' = -(len - col') \\ y' = -row' \\ \end{array} \right. \end{equation}\]结合旋转坐标关系式,我们就可以求出旋转前后矩阵索引的关系式
\[\begin{equation} \left\{ \begin{array}{l} row' = col \\ col' = -row + len\\ \end{array} \right. \end{equation}\]遍历策略
由于题目要求,原地算法,所以按顺序遍历是不可取的。由旋转的性质可知,每次像洋葱皮的形式,一圈一圈的遍历,每个循环完成这一圈的旋转
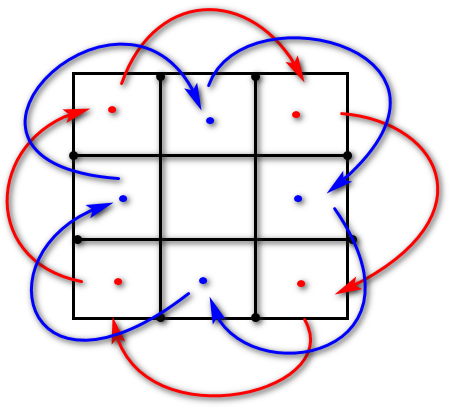
void rotate(vector<vector<int>>& matrix) {
int n = matrix.size();
for (int row = 0; row < n / 2; row++) {
for (int col = row; col < n - 1 - row; col++) {
int curRow = row;
int curCol = col;
int target = matrix[curRow][curCol];
for (int i = 0; i < 4; i++) {
int nextRow = curCol;
int nextCol = n - 1 - curRow;
swap(target, matrix[nextRow][nextCol]);
curRow = nextRow;
curCol = nextCol;
}
}
}
}
方法二
先对矩阵转置,再横向翻转,就相当于旋转了90度
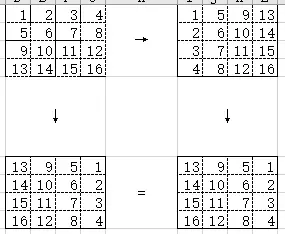
void rotate(vector<vector<int>>& matrix) {
int n = matrix.size();
// 转置
for (int row = 0; row < n; row++) {
for (int col = 0; col < row; col++) {
swap(matrix[row][col], matrix[col][row]);
}
}
// 横向翻转
for (int row = 0; row < n; row++) {
for (int col = 0; col < n / 2; col++) {
swap(matrix[row][col], matrix[row][n - 1 - col]);
}
}
}
方法三
先按照斜对角线翻转,再纵向翻转,也相当于旋转了90度。这样做比方法二好在,纵向翻转时,遍历的次数减少,只需交换数组即可
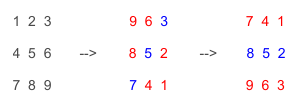
蓝色为翻转轴
void rotate(vector<vector<int>>& matrix) {
int n = matrix.size();
// 按斜对角线翻转
for (int row = 0; row < n - 1; row++) {
for (int col = 0; col < n - row - 1; col++) {
swap(matrix[row][col], matrix[n - 1 - col][n - 1 - row]);
}
}
// 纵向翻转
for (int row = 0; row < n / 2; row++) {
swap(matrix[row], matrix[n - 1 - row]);
}
}
完整代码地址
Reference
[1]赵智雄. 旋转图像[EB/OL]. 简书, 2018.
文档信息
- 本文作者:wzx
- 本文链接:https://masterwangzx.com/2019/02/19/rotate/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)