数据不平衡是机器学习中经常遇到的问题，其根本的解决方法就是收集或制造一些数据扩大数据集。但在实际情况中，收集更多的数据所需要的成本很大，所以我们通过过采样算法来生成新的数据来克服数据不平衡

简单的尝试

1. 调整分类的阀值。在二分类问题中，减少数据集偏少的那个分类的阀值，可以一定程度上缓解数据不平衡。

2. 随机升采样，即随机添加少数类中的样本，直至数据平衡。这是简单的复制样本行为，可能会导致过拟合。

SMOTE

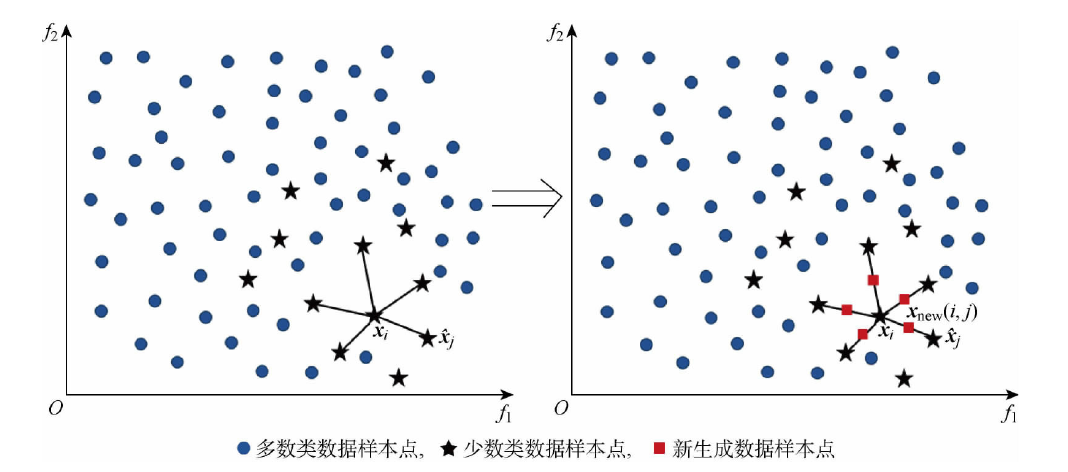
SMOTE(Synthetic Minority Oversampling Technique) 通过类似随机线性插值的方法扩大少数类数据。

对于某个少数类 $X=\{\boldsymbol{x_i}|i=1\cdots m\}$ , 通过计算欧氏距离得到某个样本点 $\boldsymbol{x_i}$ 的k个近邻。
假设需要扩大的倍数为N（k>N）。我们随机选取k个近邻中的N个近邻，分别对每个近邻 $x_j$ 用如下公式得到新的样本点

将上述过程应用到每个样本点中，最后就会返回扩大后的数据集

ADASYN

ADASYN(Adaptive Synthetic)根据数据集的总体样本分布情况来为不同的少数类样本生成不同数目的新样本。相对于SMOTE算法，其对每一个少数类样本的重视程度不同

• 计算不平衡度 假设少数类数目 $m_s$，多数类数目 $m_l$，则不平衡度

当不平衡度大于一个阀值时，我们才会采取以下操作

• 计算需要少数类中合成的样本数量

这里的 $\beta$ 用来指定想要的数据平衡度

• 对于每个少数类中的样本点，通过计算欧氏距离得到在全部数据中的k个近邻，定义以下比例，其中 $\Delta_i$为 $\boldsymbol{x_i}$ 的k个近邻中多数类样本点的个数

• 归一化

• 计算 $\boldsymbol{x_i}$ 需要产生的样本数

• 扩大样本
  对于每个少数类的样本点 $\boldsymbol{x_i}$ ，需要生成 $g_i$ 个新样本。
  在其k个近邻中，随机选取一个少数类样本 $\boldsymbol{x_{zi}}$，

以上过程循环 $g_i$ 次，最后再对每个少数类的样本点都进行上述操作

ADASYN算法的关键思想是使用密度分布 $\hat{r_i}$ 作为标准来自动确定每个少数类需要生成的合成样本的数量。 $\hat{r_i}$ 是根据少数类样本的学习难度来确定的权重，所以ADASYN会强制模型学习那些难以学习的少数类样本

代码实现

上述方式包括评价方法均已在 imbalanced-learn 中实现，可以阅读官方文档

REFERENCE

[1]CHAWLA N V, BOWYER K W, HALL L O等. SMOTE: synthetic minority over-sampling technique[J]. Journal of artificial intelligence research, 2002, 16: 321–357.

[2]HE H, BAI Y, GARCIA E A等. ADASYN: Adaptive synthetic sampling approach for imbalanced learning[C]//2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence). IEEE, 2008: 1322–1328.