如前文所述,直方图均衡能自动的确定变换函数,使图像的颜色分布更均匀。但有时这种图像增强并不是我们想要的,我们就可以运用特殊的直方图处理技术,直方图规定化,AHE,CLAHE
直方图规定化
改变原图像的灰度值概率分布,使其转变成我们想要的概率分布,这个方式就称作直方图规定化或者直方图匹配
在前文符号的基础上,设 $z$ 为输出图像的灰度值,则 $p_z(z)$ 表示其概率密度函数
我们希望能找到一种变换函数,能将原概率密度 $p_r(r)$ 转化为 $p_z(z)$,具体想法就是找到原图像与输出图像的直方图均衡化后的值作为中间变量,从而找到变化函数
对于原图像的均衡化结果
\[s=T(r)=(L-1)\int_0^r{p_r(w)dw}\]对于输出图像的均衡化结果
\[G(z)=(L-1)\int_0^z{p_z(t)dt}=s\]由 $G(z)=T(r)$ 可得
\[z=G^{-1}[T(r)]=G^{-1}(s)\]联立以上公式,便可以得到连续灰度值的转化方程
一般处理方法
上面的难点在于反函数比较难找,但我们图像一般是当做离散值来处理,这样就比较简单了
- 计算原图像的概率密度 $p_r(r)$ ,做均衡化处理 $T(r_k)$ ,并将输出值四舍五入为整数
- 对目标概率分布做均衡化处理 $G(z_q)$,并将输出值四舍五入为整数
- 将每个 $T(r_k)$ 与 $G(z_q)$ 对应起来,这样就得到了 $r_k \to z_q$ ,如果存在一对多的情况,选择最小的值
代码实现
这里使用 numpy 实现
import cv2
from matplotlib import pyplot as plt
import numpy as np
origin = cv2.imread('test.png', cv2.IMREAD_UNCHANGED)
pattern = cv2.imread('pattern.png', cv2.IMREAD_UNCHANGED)
processed = np.zeros(origin.shape, dtype=np.int)
# 直方图均衡
def get_map(img: np.ndarray):
hist, bins = np.histogram(img.flatten(), 256, [0, 256], density=True)
cdf = hist.cumsum()
cdf_m = np.ma.masked_equal(cdf, 0)
cdf_m = (cdf_m - cdf_m.min()) * 255 / (cdf_m.max() - cdf_m.min())
return np.ma.filled(cdf_m, 0).astype(np.int)
# 规定化
origin_map = get_map(origin)
pattern_map = get_map(pattern)
for i in range(origin.shape[0]):
for j in range(origin.shape[1]):
processed[i, j] = (np.abs(pattern_map - origin_map[origin[i, j]])).argmin()
plt.figure()
plt.subplot(321)
plt.axis('off')
plt.imshow(origin, cmap='gray')
plt.subplot(322)
plt.hist(origin.reshape(-1), bins=256, range=[0, 256], density=True)
plt.subplot(323)
plt.axis('off')
plt.imshow(pattern, cmap='gray')
plt.subplot(324)
plt.hist(pattern.reshape(-1), bins=256, range=[0, 256], density=True)
plt.subplot(325)
plt.axis('off')
plt.imshow(processed, cmap='gray')
plt.subplot(326)
plt.hist(processed.reshape(-1), bins=256, range=[0, 256], density=True)
plt.show()
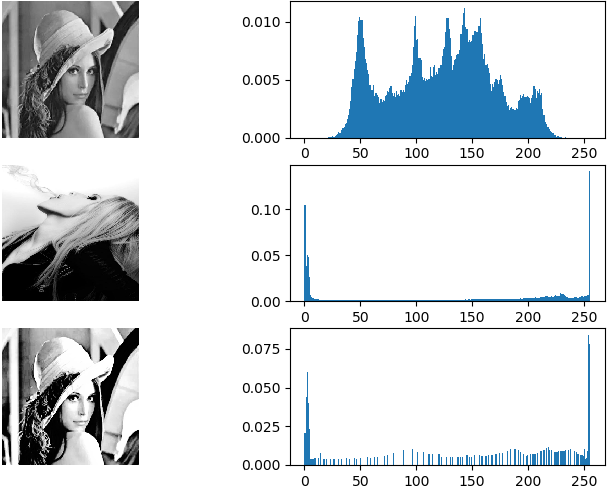
AHE
图像被分成称为“tile”的小块(在OpenCV中,tileSize默认为8x8)。然后像往常一样对这些块中的每一个进行直方图均衡。这样处理称作 AHE(Adaptive histgram equalization)。一般使用以下三种方法
- 将原始图片划分成不重叠的子块,在每个子块内做直方图处理,该方法简单但输出图像会有块效应
- 类似模板卷积的方式,以待处理的点为中心,取其邻域为子块,在子块内做直方图处理,处理结果仅映射到该点可以消除块效应,但需要对每个点计算一次直方图处理,效率低
- 前两种方法的结合版,不再逐像素移动,步长小于子块宽度以确保两个相邻子块有重叠;每个子块做直方图映射后的结果赋值给子块内所有点,这样每个点会有多次赋值,最终的取值为这些赋值的均值
但是 AHE 的缺点在于,如果子区域的灰度值近似一致时,对比度就会被过度增强,一些噪声就可能被过度放大
CLAHE
相比 AHE ,CLAHE 增加了对比度限制。如果任何直方图区间高于指定的对比度限制(在OpenCV中默认为40),则在应用直方图均衡之前,将这些像素剪切并均匀分布到其他区间 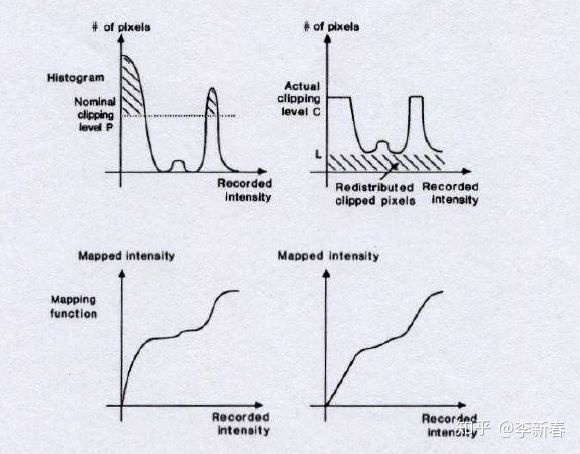
针对分块现象,应用双线性插值,对其临近的四个块的变换函数插值获取
import cv2
from matplotlib import pyplot as plt
img = cv2.imread('test2.png', cv2.IMREAD_GRAYSCALE)
clahe = cv2.createCLAHE(clipLimit=2.0, tileGridSize=(8, 8))
processed = clahe.apply(img)
plt.figure()
plt.subplot(121)
plt.axis('off')
plt.imshow(img, cmap='gray')
plt.subplot(122)
plt.axis('off')
plt.imshow(processed, cmap='gray')
plt.show()

REFERENCE
[1]OpenCV: OpenCV-Python Tutorials[EB/OL].
[2]冈萨雷斯. 数字图像处理[M]. 阮秋琦, 译. 电子工业出版社, 2011.
[3]直方图均衡化[EB/OL]. 知乎专栏.
文档信息
- 本文作者:wzx
- 本文链接:https://masterwangzx.com/2019/07/14/special-histogram/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)