静态索引结构在初始创建时就已经定型,而且在运行期间,其结构不发生变化,存取方便,但插入删除效率低。动态索引结构在运行期间,其结构随着增删而调整,以保持最佳搜索效率。B树与B+树就属于动态索引结构。

B树
定义
B树是一种平衡的多分树(多路查找树),所谓平衡就是所有叶结点的深度都趋于相等。m阶B树的定义如下:
- 每个结点至多有 $m$ 个子结点
- 除根结点和叶结点外,其它每个结点至少有 $\lceil \frac{m}{2} \rceil$ 个子结点
- 根结点至少有两个子结点,除非树中只有根结点
- 所有的叶结点在同一层(平衡)
- 有 $k$ 个子结点的非根结点恰好包含 $k-1$ 个关键码
- 结点内的关键码不重复,父结点中的关键码是子结点的分界,类似BST
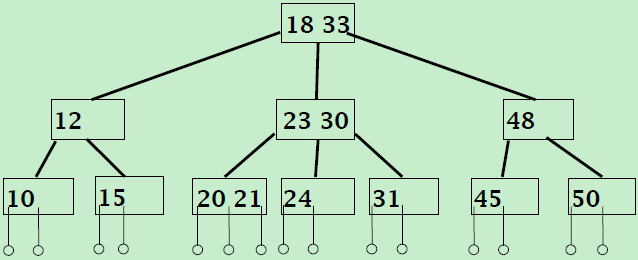
如图所示,这是一个3阶B树。特别地,3阶B树又称2-3树,4阶B树又称2-3-4树
优势
B树作为一种动态索引的数据结构,减少了访外的次数
- B树把(值接近)相关记录放在同一个磁盘页中,从而利用了访问局部性原理,磁盘预读原理
- B树保证树中至少有一定比例的结点是满的
- 改进空间利用率
- 减少检索和更新操作的磁盘读取数目
插入
B树的检索很容易,只需从根结点依次往下,对比结点内的关键码即可。如果检索到的子结点指针为空,说明已经检索到叶结点并且检索失败,这时一般就是要插入这个关键码到叶结点中。
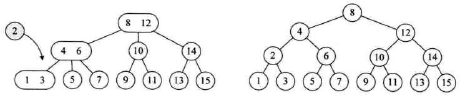
以2-3树为例,如图所示,如果要插入的叶结点是一个2结点,那么直接插入到该节点中即可,该节点升级为3结点。

考虑一种极端的情况,如果要插入的叶结点是一个3结点,并且其父结点直到根结点都为3结点,那么所有路径上的结点都需要分裂,树的高度会增加1。
如下图所示,分裂时将结点中的中间关键码插入父结点,其左右子结点调整为原先的左右关键码。依据这样的规则向上分裂,直至结点不溢出。
删除
如果删除的关键码不在叶结点层,如下图所示,则与后继结点(叶结点)交换,删除交换后的叶结点。
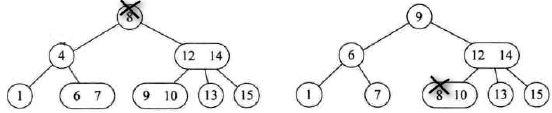
如果删除的关键码在叶结点层
- 如图1所示,如果该结点的关键码个数大于 $\lceil\frac{m}{2}\rceil-1$,直接删除即可
- 如果该结点的关键码个数等于 $\lceil\frac{m}{2}\rceil-1$
- 如图2所示,如果兄弟结点关键码个数大于 $\lceil\frac{m}{2}\rceil-1$ ,父结点中的关键码下移到该结点,兄弟结点中的一个关键码上移至父结点位置
- 如图3所示,如果兄弟结点关键码个数等于 $\lceil\frac{m}{2}\rceil-1$ ,将父结点中的关键码下移与当前结点及它的兄弟结点中的关键码合并,形成一个新的结点。这时要特别注意,B树形态的改变,如图4所示
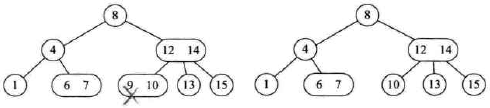 图1
图1
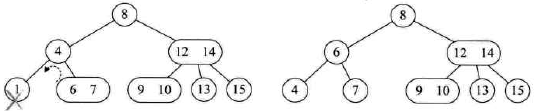 图2
图2
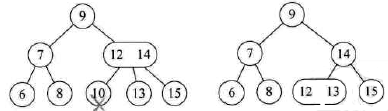 图3
图3
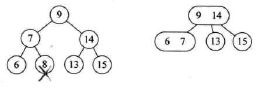 图4
图4
B+树
是B树的一种变形,相比于B树遍历更快(只需扫一遍叶结点),查询区间数据更快(缓存命中率高),检索更快(层级小),主要应用在数据库主码索引和磁盘文件管理索引
定义
如下图所示,m阶B+树定义如下:
- 每个结点至多有 $m$ 个子结点
- 每个结点(除根外)至少有 $\lceil \frac{m}{2} \rceil$ 个子结点
- 根结点至少有两个子结点
- 所有的关键码及指针均出现在叶结点上
- 各层结点中的关键码均是下一层相应结点中最大关键码(或最小关键码)的复写
- 有 $k$ 个子结点的结点必有 $k$ 个关键码

增删改查
类似B树
REFERENCE
[1]程杰. 大话数据结构[M]. 清华大学出版社, 2011.
[2]B树 - 北京大学[EB/OL]. Coursera.
[2]B+树 - 北京大学[EB/OL]. Coursera.
文档信息
- 本文作者:wzx
- 本文链接:https://masterwangzx.com/2019/12/17/b-tree/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)