图的结构要比相比二叉树和森林要更复杂

定义

$G(V,E)$ , $V$ 表示顶点(vectex)的集合，$E$ 是边(edge)的集合

组成

• 图
  • 边
    • 无向边 $(v_i,v_j)$
    • 有向边(弧arc) $<v_i,v_j>$
  • 顶点
    • 入度
    • 出度
  • 路径
    • 简单路径 (除首尾顶点外，顶点不重复出现)
    • 回路(环cycle) (首尾顶点相同)
      • 无向图中，两个顶点不能组成环

分类

• 图
  • 完全图
  • 稀疏图
    • 稀疏因子 $\delta=\frac{t}{m\times n}<0.05$
    • 边数小于完全图的5％
  • 稠密图
  • 无向图
  • 有向图
  • 带权图(网network)
  • 无环图(directed acyclic graph,DAG)
  • 有根图
    • 树
    • 森林
  • 连通图(任意顶点间都是连通的)
    • 无向图
      • 连通分量(最大连通子图)
    • 有向图
      • 强连通(任意顶点间有双向路径)
      • 强连通分量(极大强连通子图)

存储结构

$G(V,E)$ 是一个有 $n$ 个顶点的图，有 $e$ 条边

邻接矩阵

用二维数组 $A[n,n]$ 来存储图

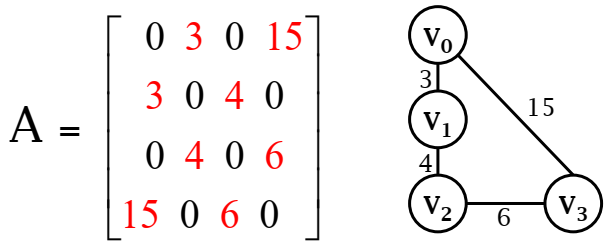
对于 n 个顶点的图，邻接矩阵的空间代价都为 $O(n^2)$，与边数无关

邻接表

• 顶点表目
  • data 顶点数据域
  • firstarc
    • 边表指针域(无向图)，顶点 $v_i$ 所有边组成的单链表
    • 出边表指针域(有向图邻接表)，顶点 $v_i$ 所有出边组成的单链表
    • 入边表指针域(有向图逆邻接表)，顶点 $v_i$ 所有入边组成的单链表
• 边(出入度)表
  • adjvex 相邻点在顶点表目的索引
  • nextarc 顶点的下一条边的指针
  • info 权重信息
• 无向图，邻接表的空间代价为 $O(n+2e)$
• 有向图，邻接表的空间代价为 $O(n+e)$

十字链表

邻接表和逆邻接表的结合

• 顶点表目
  • data 顶点数据域
  • firstinarc 入边表指针域，顶点 $v_i$ 所有入边组成的单链表
  • firstoutarc 出边表指针域，顶点 $v_i$ 所有出边组成的单链表
• 出入度表
  • tailvex 弧起点(当前顶点)在顶点表目的索引
  • tailnextarc 顶点的下一条入边的指针
  • headvex 弧终点(相邻顶点)在顶点表目的索引
  • headnextarc 顶点的下一条出边的指针
  • info 权重信息

遍历

由于图的特殊性，我们要考虑非连通图和存在回路的情况，为每个顶点保存一个标志位，存储是否访问过，即可

深度优先遍历

类似树的前序遍历，可以利用栈或者递归实现，比较简单

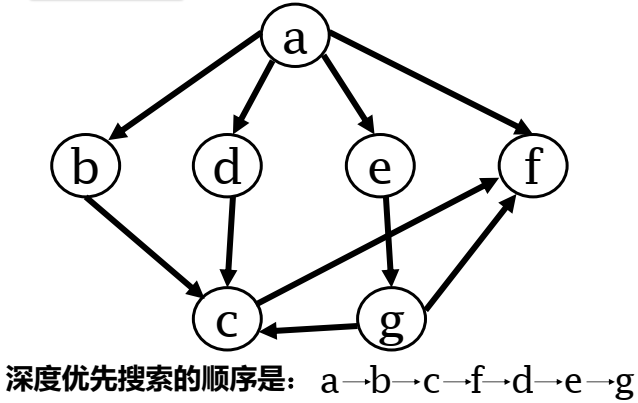
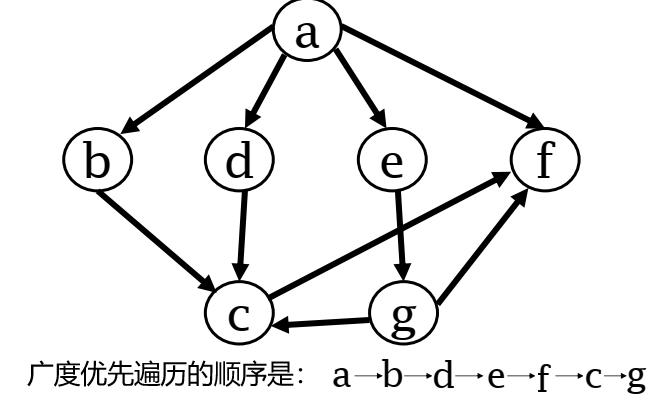
广度优先遍历

类似的，可以用队列来实现，比较简单

拓扑排序

将一个有向无环图中所有顶点在不违反先决条件关系的前提下排成线性序列的过程称为拓扑排序。在之前的博客中已经分析过了

REFERENCE

[1]图的遍历 - 北京大学[EB/OL]. Coursera.
[2]图的存储结构 - 北京大学[EB/OL]. Coursera.
[3]图的概念和抽象数据类型 - 北京大学[EB/OL]. Coursera.