WZX's Blog

图的算法

2019/11/09 算法和数据结构 共 4519 字，约 13 分钟

最短路径与最小生成树算法

最短路径

Dijkstra算法

Dijkstra 利用贪心的思想，求出所有顶点对某一源点的单源最短路径。将顶点分为两个集合，一个为未找到最短路径的顶点的集合 $U$ ，另一个为已最短路径的顶点的集合 $S$ 。重复做以下步骤

  1. 从 $U$ 取出路径长度最短的顶点 $v_i$
  2. 遍历 $U$ 中的其他顶点 $v_j$，比较 $v_j$ 原来的路径长度与经过 $v_i$ 这个中间点之后的长度，取更小的路径更新 $v_j$ 的路径长度
  3. $v_i$加入集合$S$中

之所以取出 $U$ 中路径长度最短的顶点 $v_i$ ，是因为集合 $U$ 中没有能让 $v_i$ 变小的中间点，所以这个 $v_i$ 的最短路径就是当前的路径

很明显，如果存在负权值，某些路径将会计算错误。Dijkstra算法不支持负权值的情况

我们看下面这个例子

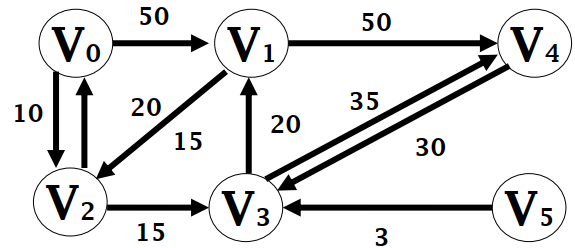
要求所有顶点到 $v_0$ 的最短距离

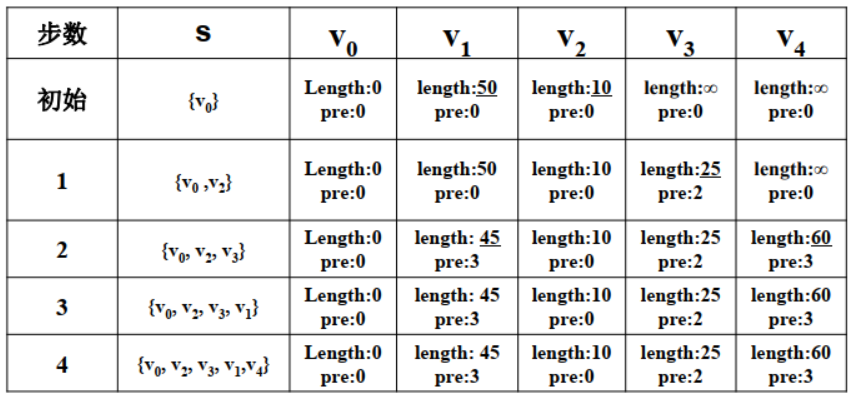
如图所示

  1. 取出拥有最短路径的 $v_2$ ，通过 $v_2$ 更新了 $v_3$ ，$v_2$ 求解完毕
  2. 取出拥有最短路径的 $v_3$ ，通过 $v_3$ 更新了 $v_1$ 和 $v_4$，$v_3$ 求解完毕
  3. 取出拥有最短路径的 $v_1$ ，$v_1$ 求解完毕
  4. 取出拥有最短路径的 $v_4$ ，$v_4$ 求解完毕

利用最小堆实现

/**
   * @param inputEdges: 有向边集合{start, end, weight}
   * @param n: 顶点个数
   * @param k: 源点编号(0, 1, ..., n - 1)
   * @return 各顶点到源点的距离
   */
public int[] dijkstra(int[][] inputEdges, int n, int k) {
  int[] dist = new int[n];
  Arrays.fill(dist, Integer.MAX_VALUE);
  // 起点->边
  Map<Integer, List<int[]>> graph = new HashMap<>();
  for (int[] edge : inputEdges) {
    graph.putIfAbsent(edge[0], new LinkedList<>());
    graph.get(edge[0]).add(edge);
  }
  // 顶点的最小堆, 存放更新好最短距离却没有更新其他顶点最短距离的顶点
  // (point, distance)
  PriorityQueue<Map.Entry<Integer, Integer>> queue = new PriorityQueue<>(
    Comparator.comparingInt(Map.Entry::getValue));
  // 添加源点
  queue.add(new AbstractMap.SimpleEntry<>(k, 0));
  dist[k] = 0;
  dist[0] = 0;
  // 标记更新好最短距离的顶点
  boolean[] visit = new boolean[n];
  // 从源点出发, 更新到其他点的最短距离
  while (!queue.isEmpty()) {
    int point = queue.poll().getKey();
    // 优先队列中可能包含重复元素(顶点可能重复添加), 防止重复
    if (visit[point]) continue;
    visit[point] = true;
    // 访问point的所有出边
    List<int[]> edges = graph.getOrDefault(point, Collections.emptyList());
    for (int[] edge : edges) {
      int next = edge[1], time = edge[2];
      if (visit[next]) continue;
      // origin -> next => min(point -> next + origin -> point)
      dist[next] = Math.min(dist[next], dist[point] + time);
      // 这里没有删除旧的next结点, 因为新的next总比旧的先访问, 由于visit数组的标记, 旧结点将被跳过
      queue.add(new AbstractMap.SimpleEntry<>(k, 0));
    }
  }

  return dist;
}

有最小堆的性质可知，最短路径顶点删除的时间复杂度为 $O(logn)$ ，入堆的时间复杂度为 $O(logn)$，所以当顶点数为 $E$ ，边数为 $V$ 时，算法的时间复杂度为 $O((E+V)logV)$，适合稀疏图

Floyd算法

弗洛伊德算法利用动态规划的想法，先保存两点间的直接距离，再用其他顶点作为中间点更新两点的距离。很明显需要通过两个循环嵌套来遍历所有的顶点对，再嵌套一个循环用来遍历所有的中间点。很明显，时间复杂度为 $O(V^3)$，适合稠密图

/**
   * @param inputEdges: 有向边集合{start, end, weight}
   * @param n: 顶点个数
   * @param k: 源点编号
   * @return 各顶点到源点的距离
   */
public int[] floyd(int[][] inputEdges, int n, int k) {
  // 邻接矩阵
  int[][] dist = new int[n][n];
  for (int i = 0; i < n; i++) {
    for (int j = 0; j < n; j++) {
      if (i != j) dist[i][j] = Integer.MAX_VALUE;
    }
  }
  // 更新直接路径
  for (int[] edge : inputEdges) {
    dist[edge[0]][edge[1]] = edge[2];
  }
  // 用每个顶点作为中间点更新原两点间的路径
  for (int v = 0; v < n; v++) {
    for (int i = 0; i < n; i++) {
      for (int j = 0; j < n; j++) {
        // 防止溢出
        if (dist[i][v] == Integer.MAX_VALUE || dist[v][j] == Integer.MAX_VALUE) continue;
        dist[i][j] = Math.min(dist[i][j], dist[i][v] + dist[v][j]);
      }
    }
  }

  return dist[k];
}

最小生成树(minimum-cost spanning MST)

最小生成树指拥有图中所有顶点，并且树的权值总和最小的树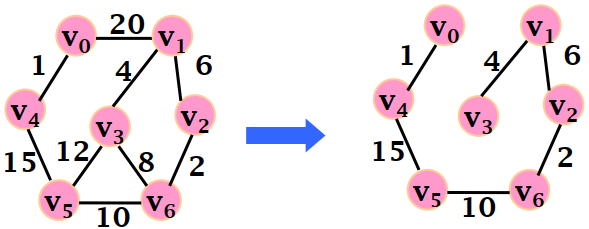

Prim算法

普里姆算法与 Dijkstra算法很类似，是贪心的算法。理解起来很简单，每次往 MST 中加入与MST距离最短的顶点，直至所有顶点加入，体现了贪心的思想。与Dijkstra算法类似地，如果采用最小堆，时间复杂度为 $O((E+V)logV)$，适合稀疏图

/**
   * @param inputEdge: 有向边集合{start, end, weight}
   * @param n: 顶点个数
   * @param k: 最小生成树顶点编号
   * @return 最小生成树的路径和
   */
private int prime(int[][] inputEdge, int n, int k) {
  int[] dist = new int[n];
  Arrays.fill(dist, Integer.MAX_VALUE);
  // 起点->边
  Map<Integer, List<int[]>> graph = new HashMap<>();
  for (int[] edge : inputEdge) {
    graph.putIfAbsent(edge[0], new LinkedList<>());
    graph.get(edge[0]).add(edge);
  }
  // 顶点的最小堆, 存放更新好最短距离却没有更新其他顶点最短距离的顶点
  // (point, distance)
  PriorityQueue<Map.Entry<Integer, Integer>> queue = new PriorityQueue<>(
    Comparator.comparingInt(Map.Entry::getValue));
  // 添加源点
  queue.add(new AbstractMap.SimpleEntry<>(k, 0));
  dist[k] = 0;
  dist[0] = 0;
  // 标记更新好最短距离的顶点
  boolean[] visit = new boolean[n];
  int res = 0;
  // 从源点出发, 更新到其他点的最短距离
  while (!queue.isEmpty()) {
    int point = queue.poll().getKey();
    // 优先队列中可能包含重复元素, 防止重复
    if (visit[point]) continue;
    visit[point] = true;
    res += dist[point];
    // 访问point的所有出边
    List<int[]> edges = graph.getOrDefault(point, Collections.emptyList());
    for (int[] edge : edges) {
      int next = edge[1], time = edge[2];
      if (visit[next]) continue;
      // origin -> next => min(point -> next + origin -> point)
      dist[next] = Math.min(dist[next], time);
      // 这里没有删除旧的next结点, 因为新的next总比旧的先访问, 由于visit数组的标记, 旧结点将被跳过
      queue.add(new AbstractMap.SimpleEntry<>(next, dist[next]));
    }
  }

  return res;
}

Kruskal算法

克鲁斯克尔算法就与 Prim算法如出一辙，但是不同的是，他每次往 MST 中加入全局最小的边，当然要判断加入边会不会产生回路，这就需要并查集来解决了。时间复杂度为 $O(ElogE+Vlog*E)$，适合稠密图

/**
   * @param inputEdges: 有向边集合{start, end, weight}
   * @param n: 顶点个数
   * @return 最小生成树的路径和
   */
public int kruskal(int[][] inputEdges, int n) {
  // 并查集, 标记mst的连通关系
  UF uf = new UF(n);
  int res = 0, num = 0;
  // 排序, 每次尝试加入最小的边
  Arrays.sort(inputEdges, Comparator.comparingInt(x -> x[2]));
  for (int[] edge : inputEdges) {
    // 边的两点连接了两个相异的连通块则可以加入mst, 否则会在mst中形成环
    if (!uf.isConnect(edge[0], edge[1])) {
      res += edge[2];
      num++;
      // mst中已有全部结点
      if (num == n) break;
      // 记录边的连通关系
      uf.union(edge[0], edge[1]);
    }
  }

  return res;
}

REFERENCE

[1]最短路径 - 北京大学[EB/OL]. Coursera.
[2]最小生成树 - 北京大学[EB/OL]. Coursera.

文档信息

Search

    Table of Contents