外排序算法的实现和比较
基本思想
外部排序指的是大文件的排序,即待排序的记录存储在外存储器上,待排序的文件无法一次装入内存,需要在内存和外部存储器之间进行多次数据交换,以达到排序整个文件的目的。
假设待排的记录有m个,内存大小为n,最简单的思想就是,每次从外存中取出n个记录,利用内排序算法排序,再输出到外存中,这样就得到了 $\lfloor \frac{m}{n} \rfloor$ 个顺串。两两归并所有顺串,就得到了最终的结果。
但是这种方法明显是低效的。为了减少归并的次数,访问外存的次数,我们可以减少顺串的数量,合理安排归并顺序,增加单次归并的顺串数,通过以下方式实现。
置换选择排序
通过堆选择的方式,减少顺串的数量。假设内存中只能存放三个记录,待排记录为80 92 12 97 13 34 18 89 27 57 40 74。
- 读入三个数据,建立最小堆
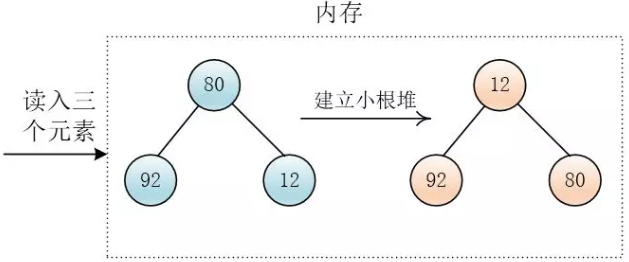
- 将堆顶元素输出到外存
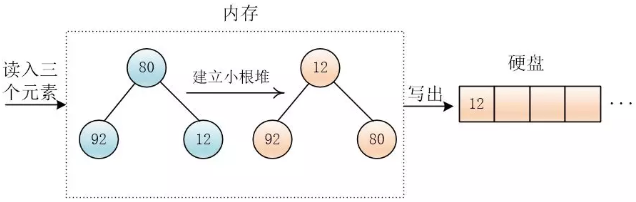
- 读入下一条记录,如果大于堆顶,则覆盖堆顶,并用
siftDown调整最小堆
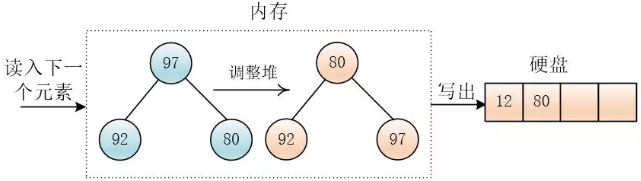
- 如果记录小于堆顶,将堆尾元素覆盖根结点,将记录放入堆尾,并将堆的大小-1,即将这条记录排除堆外
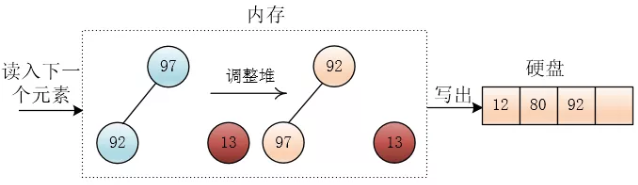
- 重复234步骤,直至堆为空,这是一个顺串就完成了
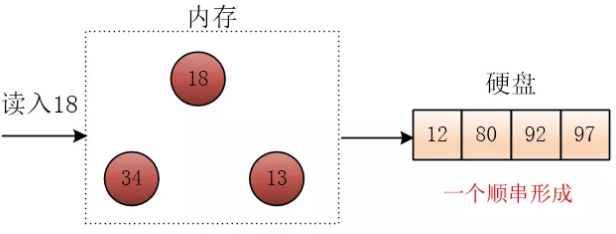
- 对内存中的记录,重建最小堆,重复以上步骤,直至完成全部顺串
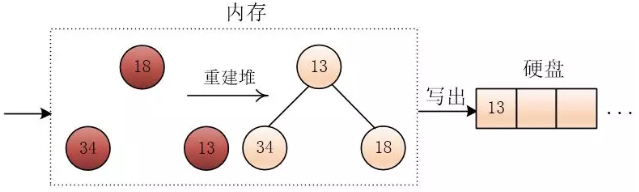
置换选择排序算法得到的顺串长度并不相等。如果堆的大小为M,则顺串的最小长度为M,最好情况是得到一个顺串。平均情况是顺串的长度为2M(铲雪机模型)。
具体实现参考 cousera 上高级数据结构与算法的课后题的解答
败者树
可以利用k路归并来增加单次归并的顺串数,每次将k个顺串合并成一个顺串,k越大,外存读写的次数就越小。简单地,我们直接对内存中的元素扫一遍获取最小元素,但是k的增大会增加内部归并的时间,所以使用选择树来实现k路归并,减少内部归并的时间。
如下图所示,胜者树中叶结点中存放顺串的首个元素,分支结点中的值都表示的是左右子结点相比较后的较小值(胜者)。
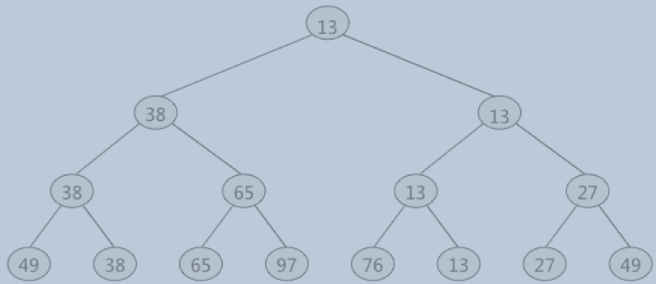
每次弹出最终胜利的叶结点后,需要压入新的叶结点,这时就需要对胜者树重构。将新加入的叶结点与兄弟结点比较,由下往上依次类似上升比较,所以胜者树每上升一次需要访问两个节点,父结点和兄弟结点。
与胜者树类似的是败者树,败者树上升一次只需访问父结点。虽然两棵树上升一次的时间复杂度是一样的,但是现在程序的主要瓶颈在于访存,所以败者树相较于胜者树减少了访存的时间,也就有了性能优势。
败者树与胜者树一样,每次比较都是用胜者比较,但是存储的是失败者,有点不好理解,以下图为例。一颗5-路归并的败者树,b0至b4为待归并数组,由于败者树是完全二叉树,所以败者树的分支结点用数组ls在内存中表示,败者树中存储失败数组的索引。
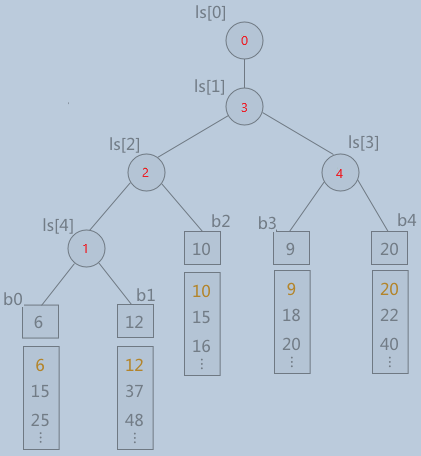
由图可知,b0[0]比b1[0]小,ls[4]存储败者1。ls[4]的胜者b0[0]小于b2[0],ls[2]存储败者2,依次类推,直到ls[1]。ls[0]则存储未失败过的冠军0。下一次归并,导入b0[1]并对败者树进行重构,不断同其父结点进行比较,败者留在父结点中,胜者继续向上比较即可。
为什么重构时只需与父结点比较呢?首先明确一点,父结点肯定是失败者,肯定是另一侧子树的胜利者,因为当前侧中存在上一届总冠军。这样的话,当前结点(当前侧的胜利者)与父结点比较就是与另一侧的胜利者比较,这与建树时的方法一致。
可以明显看出,无论使用胜者树还是败者树,一次内部归并的时间复杂度都是 $O(logk)$。一般来说,使用最小堆可以实现相同的时间复杂度,但是使用胜者/败者树性能更优。因为调整堆的时候,每次都要选出父结点的两个子结点的最小值,然后再用最小值和父结点进行比较,所以每调整一层需要比较两次。使用胜者/败者树每次调整只需与其兄弟/父结点比较,这样就少了一半的比较次数。
K-路最佳归并树
使用k-哈夫曼树合理安排归并顺序可以减少访问外存的次数。以顺串为结点,长度为权值,建立赫夫曼树。如下图所示,赫夫曼树使加权路径和最短,也就是所有k-路归并的读写次数总和最小。注意,使用权值为0的虚段填充k叉树
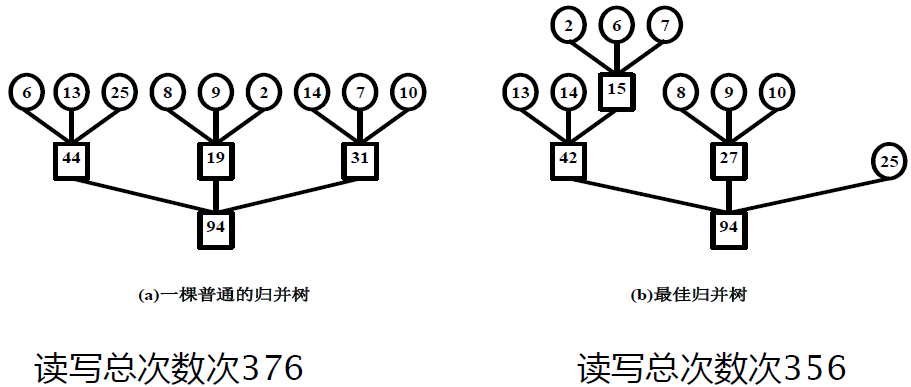
代码实现
若归并后的序列长为 $n$,直接k路归并算法时间复杂度为 $\Theta(kn)$,使用败者树实现的时间复杂度为 $\Theta(k+nlogk)$
- 使用置换选择排序算法生成等待归并的顺串
- 使用k-哈夫曼树合理安排归并顺序,形成K-路最佳归并树
- 每次归并使用败者树实现 这就是外排序的基本思路,下面是代码实现
class LoserTree {
private:
int maxSize; // 最大选手数
int n; // 选手个数
int* ls; // 分支结点数组(索引)
int* b; // 叶结点数组(外部序列的首个元素)
int exSize; // 最底层外部结点个数
int offset; // 最底层外部结点之上的结点个数
void play(int inParent, int exLeft, int exRight);
public:
// 败者树的分支节点数与叶结点数相等
LoserTree(int treeSize) { ls = new int[treeSize]; this->maxSize = treeSize; }
~LoserTree() { delete[]ls; }
void initialize(int a[], int size);
void replay(int i);
int getWinner() { return n ? ls[0] : 0; }
};
// inParent:父结点索引(分支结点) exLeft:左子结点的外部序列索引 exRight:右子结点的外部序列索引
void LoserTree::play(int inParent, int exLeft, int exRight) {
// 失败者存入父结点
ls[inParent] = b[exLeft] > b[exRight] ? exLeft : exRight;
int exWinner = b[exLeft] <= b[exRight] ? exLeft : exRight;
// initialize的顺序是从左至右的外部序列两两比较,没必要对左分支和右分支处理的时候都上升比较
// 只对右分支上升比较一次
while (inParent > 1 && inParent % 2 != 0) {
// 这里的完全二叉树是从b[1]开始的,所以父结点为 inParent/2
int temp = b[exWinner] <= b[ls[inParent / 2]] ? exWinner : ls[inParent / 2];
// 胜者每次与父结点比较
ls[inParent / 2] = b[exWinner] > b[ls[inParent / 2]] ? exWinner : ls[inParent / 2];
// 胜者向上传递
exWinner = temp;
inParent /= 2;
}
// 把胜者存到祖父结点,等待下一次右分支的胜者与其比较
// inParent=1时,ls[0]=winner
ls[inParent / 2] = exWinner;
}
void LoserTree::initialize(int a[], int size) {
if (size < 2 || size > maxSize) {
// 出错,抛出异常
return;
}
this->n = size;
this->b = a;
// 计算最底层外部结点个数
this->exSize = 2 * n - pow(2, int(log(2 * n) / log(2)));
// 为了便于计算最底层外部结点的父结点索引,所以求offset
this->offset = pow(2, int(log(2 * n) / log(2)));
// 最底层和次底层的外部结点需要分开处理,以应对内部节点和外部结点比较的情况
// 以及确定父结点位置
for (int i = 1; i < this->exSize; i += 2) {
play((i + this->offset) / 2, i - 1, i);
}
// 次底层的外部结点的首位
int start = this->exSize + 1;
if (n % 2 != 0) {
play((n - 1) / 2, ls[(n - 1) / 2], this->exSize);
// 次底层的外部结点有一个与内部结点比较了
// 所以次底层的结点间比较的起始点+1
start++;
}
// 次底层的外部结点
for (int i = start; i < n; i += 2) {
play((i - this->exSize + n - 1) / 2, i - 1, i);
}
}
// 第i个外部叶结点改变了
void LoserTree::replay(int i) {
if (i < 0 || i > this->n) {
// 出错,抛出异常
return;
}
// 父结点位置
int inParent = 0;
if (i < this->exSize) {
inParent = (i + offset) / 2;
} else {
inParent = (i - this->exSize + n) / 2;
}
int exWinner = b[i] <= b[ls[inParent]] ? i : ls[inParent];
ls[inParent] = b[i] > b[ls[inParent]] ? i : ls[inParent];
while (inParent / 2 >= 1) {
int temp = b[exWinner] <= b[ls[inParent / 2]] ? exWinner : ls[inParent / 2];
ls[inParent / 2] = b[exWinner] > b[ls[inParent / 2]] ? exWinner : ls[inParent / 2];
exWinner = temp;
inParent /= 2;
}
ls[0] = exWinner;
}
// 这部分省略从外存读取的部分
int main(int argc, char *argv[]) {
// 待归并外部数据
ExternData data;
// 5-路最佳归并树
int k = 5;
// 每次从外存中读取长度最短的k个数组归并,就组成了k-哈夫曼树
while(!data.empty()){
int* b = data.getMinLength(k);
LoserTree loserTree(k);
loserTree.initialize(b, k);
int minIndex = loserTree.getWinner();
while(b[minIndex] != number_limits<int>::max()){
// 将归并好的元素写出
data.write(b[minIndex]);
if(data.hasNext(minIndex)){
// 读取外存中的元素
data.read(b[minIndex],minIndex);
}else{
// 标记为最大数,表示空
b[minIndex] = number_limits<int>::max();
}
loserTree.replay(minIndex);
}
}
return 0;
}
程序的难点是下标的确定,可以结合败者树的那张图片分析
LeetCode上有一道类似的题目,23. Merge k Sorted Lists。这题不是从外存中读数据了,所以k-路最佳归并树没有那么重要了。但是对于k-路归并而言,败者树在时间复杂度上还有有很大的优势的,题解
REFERENCE
[1]外排序. 趣谈编程. 微信公众平台[EB/OL].
[2]多路平衡归并排序算法. 数据结构与算法[EB/OL].
[3]外排序 - 北京大学[EB/OL]. Coursera.
文档信息
- 本文作者:wzx
- 本文链接:https://masterwangzx.com/2019/11/30/outer-sort/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)